The Euler and de Moivre's formulas. The n-th root of a complex number.

Euler's formulas:

$$\cos \phi =\frac{e^{i\phi }+e^{-i\phi }}{2};\sin \phi =\frac{e^{i\phi }-e^{-i\phi }}{2i}$$

De Moivre's formula

If $z=r{e}^{i\phi }$, then $$z^n=r^n{e}^{in\phi },$$or, in trigonometric form:

$$z^n=r^n(\cos n\phi +i\sin n\phi ).$$

Let $a=r{e}^{i\phi }$, $a\ne 0$, be a fixed complex number. Then the equation $z^n=a$, $n\in \mathbb{N}$, has exactly $n$ distinct solutions $z_0,z_1,...,z_{n-1}$, and these solutions are given by the formula $$z_k=\sqrt[n]{r}{e}^{i(\frac{\phi }{n}+\frac{2\pi }{n}k)}=\sqrt[n]{r}(\cos \frac{\phi +2\pi k}{n}+i\sin \frac{\phi +2\pi k}{n}),$$ $$k=0,1,...,n-1.$$(Here $\sqrt{r}$ is a real positive number) The numbers $z_k$, $k=0,1,...,n-1$, are called the $n$th roots of the complex number $a$ and are denoted by the symbol $\sqrt[n]{a}$.

Examples:

1. Prove Euler's formula $\cos \phi =\frac{e^{i\phi }+e^{-i\phi }}{2}$.

Solution.

It is known that $e^{i\phi }=\cos \phi +i\sin \phi$. Accordingly, $e^{-i\phi }=\cos (-\phi )+i\sin (-\phi )=\cos \phi -i\sin \phi$.

From this, we find $e^{i\phi }+e^{-i\phi }=\cos \phi +i\sin \phi +\cos \phi -i\sin \phi =2\cos \phi$.

Therefore, $\cos \phi =\frac{e^{i\phi }+e^{-i\phi }}{2}$. This is what needed to be proven.

Using de Moivre's formula, compute the following expressions:

2. $(1+i{)}^{10}$.

Solution.

Let's express the number $z=1+i$ in exponential form:

$r=\sqrt{x^2+y^2}=\sqrt{1+1}=\sqrt{2}$.

Since the number $z$ lies in the first quadrant, we have:

$\tan \phi =\frac{y}{x}=\frac{1}{1}=1$. And $\phi =\frac{\pi }{4}$.

Thus, we can express the number $z=1+i$ in exponential form: $z=\sqrt{2}{e}^{i\frac{\pi }{4}}$.

Now, using de Moivre's formula, we can find $z^{10}$:

$$(1+i{)}^{10}=(\sqrt{2}{e}^{i\frac{\pi }{4}}{)}^{10}=(\sqrt{2}{)}^{10}{e}^{i\frac{10\pi }{4}}=$$

$$=32e^{i\frac{5\pi }{2}}=32(\cos \frac{5\pi }{2}+i\sin 5\pi 2)=32i.$$

Answer: $(1+i{)}^{10}=32i.$

3. Using de Moivre's formula, express the function $\cos 3\phi$ in terms of $\cos \phi$ and $\sin \phi$.

Solution.

$$\cos 3\phi =\frac{e^{3i\phi }+e^{-3i\phi }}{2}=\frac{1}{2}((\cos \phi +i\sin \phi {)}^3+(\cos (-\phi )+i\sin (-\phi ){)}^3)=$$

$$=\frac{1}{2}({\cos }^3\phi +3i{\cos }^2\phi \sin \phi +3i^2\cos \phi {\sin }^2\phi +i^3{\sin }^3\phi +$$

$$+{\cos }^3(-\phi )-3i{\cos }^2(-\phi )\sin (-\phi )+3i^2\cos (-\phi ){\sin }^2(-\phi )-i^3{\sin }^3(-\phi ))=$$ $$=\frac{1}{2}({\cos }^3\phi +3i(1-{\sin }^2\phi )\sin \phi -3\cos \phi (1-{\cos }^2\phi )-i{\sin }^3\phi +$$ $$+{\cos }^3\phi +3i(1-{\sin }^2\phi )\sin \phi -3\cos \phi (1-{\cos }^2\phi )-i{\sin }^3\phi )=$$ $$={\cos }^3\phi +3i\sin \phi -3i{\sin }^3\phi -3\cos \phi +3{\cos }^3\phi -i{\sin }^3\phi =$$ $$=4{\cos }^3\phi -3\cos \phi +3i\sin \phi -4i{\sin }^3\phi .$$

Answer: $4{\cos }^3\phi -3\cos \phi +3i\sin \phi -4i{\sin }^3\phi .$

4. Find and plot on the complex plane all roots of the 2nd, 3rd, and 4th powers of unity.

Solution.

Let's express the number 1 in exponential form:

$1=1e^{0i}$. That is, $r=1,\phi =0$.

Next, using de Moivre's formula, we calculate the square root of unity:

$$z_0=\sqrt[2]{1}{e}^{i(\frac{0}{2}+\frac{2\pi }{2}0)}=e^0=1.$$$$z_1=\sqrt[2]{1}{e}^{i(\frac{0}{2}+\frac{2\pi }{2}1)}=e^{i\pi }=\cos \pi +i\sin \pi =-1.$$

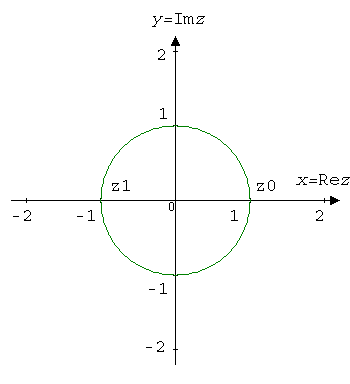
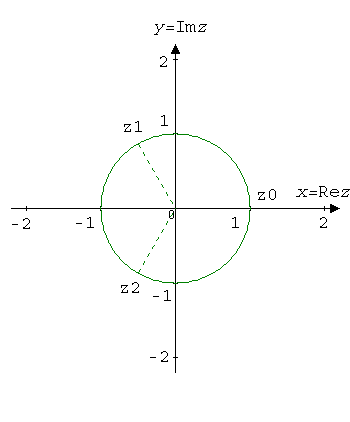
We calculate the cube root of unity:

$$z_0=\sqrt[3]{1}{e}^{i(\frac{0}{3}+\frac{2\pi }{3}0)}=e^0=1.$$

$$z_1=\sqrt[3]{1}{e}^{i(\frac{0}{3}+\frac{2\pi }{3}1)}=e^{i\frac{2\pi }{3}}=\cos \frac{2\pi }{3}+i\sin \frac{2\pi }{3}=-\frac{1}{2}+i\frac{\sqrt{3}}{2}.$$

$$z_2=\sqrt[3]{1}{e}^{i(\frac{0}{3}+\frac{2\pi }{3}2)}=e^{i\frac{4\pi }{3}}=\cos \frac{4\pi }{3}+i\sin \frac{4\pi }{3}=-\frac{1}{2}-i\frac{\sqrt{3}}{2}.$$

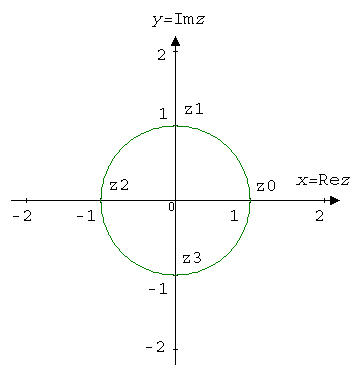
We calculate the fourth root of unity:

$$z_0=\sqrt[4]{1}{e}^{i(\frac{0}{4}+\frac{2\pi }{4}0)}=e^0=1.$$

$$z_1=\sqrt[4]{1}{e}^{i(\frac{0}{4}+\frac{2\pi }{4}1)}=e^{i\frac{\pi }{2}}=\cos \frac{\pi }{2}+i\sin \frac{\pi }{2}=i.$$

$$z_2=\sqrt[4]{1}{e}^{i(\frac{0}{4}+\frac{2\pi }{4}2)}=e^{i\pi }=\cos \pi +i\sin \pi =-1.$$

$$z_3=\sqrt[4]{1}{e}^{i(\frac{0}{4}+\frac{2\pi }{4}3)}=e^{i\frac{3\pi }{2}}=\cos \frac{3\pi }{2}+i\sin \frac{3\pi }{2}=-i.$$

Answer: Roots of the second power: $z_0=1;,,z_1=-1.$ Roots of the third power: $z_0=1;,,z_1=-\frac{1}{2}+i\frac{\sqrt{3}}{2};,,z_2=-\frac{1}{2}-i\frac{\sqrt{3}}{2}.$ Roots of the fourth power: $z_0=1;,,z_1=i;,,z_2=-1;,,z_3=-i.$

Find all values of the roots:

5. $\sqrt{-1+i\sqrt{3}}$.

Solution.

Let's express the number $z=-1+i\sqrt{3}$ in exponential form:

$r=\sqrt{x^2+y^2}=\sqrt{1+3}=2$.

Since the number $z$ lies in the second quadrant, we have:

$\tan \phi =\frac{y}{x}=\frac{\sqrt{3}}{-1}=-\sqrt{3}$ and $\phi =\frac{2\pi }{3}$.

Thus, we can express the number $z=-1+i\sqrt{3}$ in exponential form: $z=2e^{i\frac{2\pi }{3}}$.

Using de Moivre's formula, we calculate the square root of unity:

$$z_0=\sqrt{2}{e}^{i(\frac{2\pi }{6}+\frac{2\pi }{2}0)}=\sqrt{2}{e}^{i\frac{\pi }{3}}=\sqrt{2}(cos\frac{\pi }{3}+i\sin \frac{\pi }{3})=\sqrt{2}(\frac{1}{2}+i\frac{\sqrt{3}}{2}).$$

$$z_1=\sqrt{2}{e}^{i(\frac{2\pi }{6}+\frac{2\pi }{2}1)}=\sqrt{2}{e}^{i\frac{\pi }{3}+\pi }=\sqrt{2}(cos\frac{4\pi }{3}+i\sin \frac{4\pi }{3})=$$ $$=\sqrt{2}(-\frac{1}{2}-i\frac{\sqrt{3}}{2}).$$

Answer: $\pm \frac{\sqrt{2}}{2}(1+i\sqrt{3})$

6 $\sqrt[5]{-1-i}.$

Solution.

Let's express the number $z=-1-i\sqrt{3}$ in exponential form:

$r=\sqrt{x^2+y^2}=\sqrt{1+3}=2$.

Since the number $z$ lies in the third quadrant, we have:

$\tan \phi =\frac{y}{x}=\frac{-\sqrt{3}}{-1}=\sqrt{3}$ and $\phi =\frac{5\pi }{3}$.

Thus, we can express the number $z=-1-i\sqrt{3}$ in exponential form: $z=2e^{i\frac{5\pi }{3}}$.

Using de Moivre's formula, we calculate the square root of unity:

$$z_0=\sqrt[5]{\sqrt{2}}{e}^{i(\frac{5\pi }{4\cdot 5}+\frac{2\pi }{5}0)}=\sqrt[10]{2}{e}^{i\frac{\pi }{4}}=\sqrt[10]{2}(\cos \frac{\pi }{4}+i\sin \frac{\pi }{4})=\sqrt[10]{2}(\frac{1}{\sqrt{2}}+i\frac{1}{\sqrt{2}}).$$

$$z_1=\sqrt[5]{\sqrt{2}}{e}^{i(\frac{5\pi }{4\cdot 5}+\frac{2\pi }{5}1)}=\sqrt[10]{2}{e}^{i\frac{\pi }{4}}=\sqrt[10]{2}(\cos \frac{13\pi }{20}+i\sin \frac{13\pi }{20}).$$

$$z_2=\sqrt[5]{\sqrt{2}}{e}^{i(\frac{5\pi }{4\cdot 5}+\frac{2\pi }{5}2)}=\sqrt[10]{2}{e}^{i\frac{21\pi }{20}}=\sqrt[10]{2}(\cos \frac{21\pi }{20}+i\sin \frac{21\pi }{20}).$$

$$z_3=\sqrt[5]{\sqrt{2}}{e}^{i(\frac{5\pi }{4\cdot 5}+\frac{2\pi }{5}3)}=\sqrt[10]{2}{e}^{i\frac{29\pi }{20}}=\sqrt[10]{2}(\cos \frac{29\pi }{20}+i\sin \frac{29\pi }{20}).$$

$$z_4=\sqrt[5]{\sqrt{2}}{e}^{i(\frac{5\pi }{4\cdot 5}+\frac{2\pi }{5}4)}=\sqrt[10]{2}{e}^{i\frac{37\pi }{20}}=\sqrt[10]{2}(\cos \frac{37\pi }{20}+i\sin \frac{37\pi }{20}).$$

Answer: $\sqrt[10]{2}(\cos (\frac{\pi }{4}+\frac{2\pi }{5}k)+i\sin (\frac{\pi }{4}+\frac{2\pi }{5}k)).$

Homework:

1. Prove Euler's formula $\sin \phi =\frac{e^{i\phi }-e^{-i\phi }}{2i}$.

Using de Moivre's formula, calculate the following expressions:

2. $\frac{(1+i{)}^5}{(1-i{)}^3}$.

Answer: $2.$

3 $(1+i{)}^8(1-i\sqrt{3}{)}^{-6}$.

Answer: $\frac{1}{4}.$

Using de Moivre's formula, express the following functions in terms of $\cos \phi$ and $\sin \phi$:

4. $\sin 3\phi$.

Answer: $3\sin \phi -4{\sin }^3\phi .$

5. $\cos 4\phi$.

Answer: ${\cos }^4\phi -6{\cos }^2\phi {\sin }^2\phi +{\sin }^4\phi .$

Find all values of the roots:

6. $\sqrt{i}$

Answer: $\pm \frac{\sqrt{2}}{2}(1+i).$

7. $\sqrt{-1}$.

Answer: $\pm \frac{\sqrt{2}}{2}(1+i),$ $\pm \frac{\sqrt{2}}{2}(1-i).$

8. $\sqrt[4]{2\sqrt{3}+2i}$.

Answer: $\sqrt{2}(\cos (\frac{\pi }{24}+\frac{\pi }{2}k)+i\sin (\frac{\pi }{24}+\frac{\pi }{2}k)).$

9. $\sqrt[6]{1+i\sqrt{3}}$.

Answer: $\sqrt[6]{2}(\cos (\frac{\pi }{18}+\frac{\pi }{3}k)+i\sin (\frac{\pi }{18}+\frac{\pi }{3}k)).$

Tags: De Moivre's formula, Euler's formulas, complex numbers