The equation of an ellipse, hyperbola, and parabola in the polar coordinate system.
Literature: Collection of problems in mathematics. Part 1. Edited by A.V. Efimov, B.P. Demidovich.
Example.
Let $\Gamma$ be an ellipse, a branch of a hyperbola, or a parabola, $F$ be the focus of this curve, and $D$ be the corresponding directrix. Derive the equation of the curve $\Gamma$ in the polar coordinate system, where the pole coincides with the focus and the polar axis is parallel to the curve's axis (see Figure 1).
Solution.
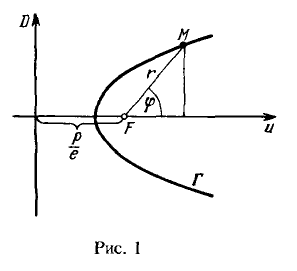
The general property of an ellipse, hyperbola, and parabola is as follows.
$$M\in\Gamma\Leftrightarrow\frac{\rho(M, F)}{\rho(M, D)}=const=e,\qquad\qquad (1)$$ where $e$ is the eccentricity of the curve ($e<1$ for an ellipse, $e>1$ for a hyperbola, and $e=1$ for a parabola).
Let's denote the distance from the focus to the directrix as $\frac{p}{e}$ ($p$ is the parameter of the curve, called the semi-focal parameter). Then, from Figure 1, it follows that $\rho(M, F)=r$ and $\rho(M, D)=\frac{p}{e}+r\cos\varphi.$ Substituting these expressions into (1), we obtain $$\frac{r}{\frac{p}{e}+r\cos\varphi}=e,$$ from which we deduce $$r=\frac{p}{1-e\cos\varphi}.\qquad\qquad (2)$$ The equation (2) is the desired polar equation in the polar coordinate system, which is general for an ellipse, hyperbola, and parabola.
Example.
2.321(a).
For the ellipse $\frac{x^2}{25}+\frac{y^2}{16}=1$, write the polar equation, assuming that the polar axis is parallel to the x-axis, and the pole is located at the left focus.
Solution.
Let's find the eccentricity of the ellipse and the parameter $p$:
$a=5$, $b=4$, $c=\sqrt{a^2-b^2}=\sqrt{25-16}=3$.
$e=\frac{c}{a}=\frac{3}{5}$.
The distance from the focus to the directrix $\frac{p}{e}=\frac{a}{e}-c\Rightarrow p=e\left(\frac{a}{e}-c\right)\Rightarrow p=\frac{3}{5}\left(\frac{5}{\frac{3}{5}-3}\right)=\frac{3}{5}\cdot\frac{25-9}{3}=\frac{16}{5}$.
Next, by substituting the found parameters into the polar equation (2) obtained in the previous problem, we will find the equation of this ellipse:
$$r=\frac{\frac{16}{5}}{1-\frac{3}{5}\cos\varphi}=\frac{16}{5-3\cos\varphi}.$$
Answer: $r=\frac{16}{5-3\cos\varphi}.$
2.324(а).
To write the canonical equation of the curve of the second order $r=\frac{9}{5-4\cos\varphi}.$ ..
Solution:
We'll transform the given equation into the form $r=\frac{p}{1-e\cos\varphi}$.
$$r=\frac{9}{5-4\cos\varphi}=\frac{9}{5(1-\frac{4}{5}\cos\varphi)}=\frac{\frac{9}{5}}{1-\frac{4}{5}\cos\varphi}.$$
From here we have: $e=\frac{4}{5},$ $p=\frac{9}{5}.$ Since $e<1,$ this curve is an ellipse.
Next, substituting the expressions for the eccentricity and the parameter by definition, we find the semi-axes of the ellipse:
$$e=\frac{c}{a}=\frac{4}{5}\Rightarrow 5c=4a;$$
$$\frac{p}{e}=\frac{a}{e}-c\Rightarrow \frac{9}{4}=\frac{a}{4/5}-c=\frac{5a-4c}{4}\Rightarrow 9=5a-4c.$$
Let's solve the system of equations. $$\left\{\begin{array}{lcl}5c=4a\\5a-4c=9\end{array}\right.\left\{\begin{array}{lcl}c=\frac{4}{5}a\\5a-\frac{16}{5}a=9\end{array}\right.\left\{\begin{array}{lcl}c=\frac{4}{5}a\\\frac{9}{5}a=9\end{array}\right.\left\{\begin{array}{lcl}c=4\\a=5\end{array}\right.\Rightarrow$$
$$b=\sqrt{a^2-c^2}=\sqrt{25-16}=3.$$
Thus, we can write the canonical equation of the ellipse as:
$$\frac{x^2}{25}+\frac{y^2}{9}=1.$$
Answer: $\frac{x^2}{25}+\frac{y^2}{9}=1.$
2.326.
To derive the polar equation of the hyperbola $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1,$ under the condition that the polar axis is aligned with the $x$-axis, and the pole is at the center of the hyperbola.
Solution.
Since the pole is at the center of the hyperbola, then $OM=r,$ hence $\rho(M, D)=r\cos\varphi-\frac{a}{e},$ $\rho(M, F)=\sqrt {(r\sin\varphi)^2+(c-r\cos\varphi)^2}.$
Thus, from equation (1), we find:
$$M\in\Gamma\Leftrightarrow\frac{\rho(M, F)}{\rho(M, D)}=const=e\Rightarrow\frac{\sqrt{(r\sin\varphi)^2+(c-r\cos\varphi)^2}}{r\cos\varphi-\frac{a}{e}}=e\Rightarrow$$
$$\Rightarrow\frac{\sqrt{r^2+c^2-2rc\cos\varphi}}{r\cos\varphi-\frac{a}{e}}=e\Rightarrow $$
$$\Rightarrow r^2+c^2-2rc\cos\varphi=(er\cos\varphi-a)^2\Rightarrow$$
$$\Rightarrow r^2+c^2-2rc\cos\varphi=e^2r^2\cos^2\varphi-2er\cos\varphi+a^2\Rightarrow$$
$$\Rightarrow r^2(1-e^2\cos^2\varphi)-2rc\cos\varphi+2rc\cos\varphi=a^2-c^2=-b^2\Rightarrow$$
$$\Rightarrow r^2=\frac{b^2}{1-e^2\cos^2\varphi}.$$
Answer: $\Rightarrow r^2=\frac{b^2}{1-e^2\cos^2\varphi}.$
Homework.
2.321(b) For the ellipse $\frac{x^2}{25}+\frac{y^2}{16}=1,$ write the polar equation, assuming that the polar axis is aligned with the $x$-axis, and the pole is at the right focus.
Answer: $r=\frac{16}{5+3\cos\varphi}.$
2.322. For the right branch of the hyperbola $\frac{x^2}{16}-\frac{y^2}{9}=1,$ write the polar equation, assuming that the polar axis is aligned with the $x$-axis,
a) at the left focus, b) at the right focus.
Answer: a) $r=-\frac{9}{4-5\cos\varphi},$ b) $r=\frac{9}{4-5\cos\varphi}.$
2.323. For the parabola $y^2=6x,$ write the polar equation, assuming that the polar axis is aligned with the $x$-axis, and the pole is at the focus of the parabola.
Answer: $r=\frac{3}{1-\cos\varphi}.$
2.324 (b, c) Write the canonical equations of the following second-order curves:
b) $r=\frac{9}{4-5\cos\varphi},$ c) $r=\frac{3}{1-\cos\varphi}.$
Answer: a) $\frac{x^2}{16}-\frac{y^2}{9}=1,$ b) $y^2=6x.$
2.327. Derive the polar equation of the parabola $y^2=2px$ under the condition that the polar axis is aligned with the $x$-axis, and the pole is at the vertex of the parabola.
Answer: $r=\frac{2p\cos\varphi}{\sin^2\varphi}.$
Tags:
