Polar, cylindrical, and spherical coordinate systems. Transition formulas.
Polar coordinates.
A polar coordinate system is a two-dimensional coordinate system in which each point on the plane is determined by two numbers - the polar angle and the polar radius.
The polar coordinate system is defined by a ray, which is called the zero or polar axis. The point from which this ray emanates is called the origin or pole. Any point on the plane is determined by two polar coordinates: radial and angular. The radial coordinate (usually denoted as $r$) corresponds to the distance from the point to the origin. The angular coordinate, also called the polar angle and denoted as $\varphi$, is the angle that must be rotated counterclockwise from the polar axis to reach this point.
$$x=\rho \cos\varphi,\; y=\rho\sin\varphi,\quad (\rho\geq 0,\,\,\,0\leq\varphi\leq 2\pi)$$
Generalized polar coordinates.$$ x=a\rho\cos\varphi,\; y=b\rho\sin\varphi,\quad (\rho\geq0, 0\leq\varphi\leq 2\pi)$$
Cylindrical coordinates:
A cylindrical coordinate system is a three-dimensional coordinate system that extends the polar coordinate system by adding a third coordinate (usually denoted as $z$), which specifies the height of the point above the plane.
$x=\rho\cos\varphi,\;y=\rho\sin\varphi,z=h,$ $ (\rho\ge 0,\, 0\le\varphi\le 2\pi,\, -\infty< h<+\infty).$
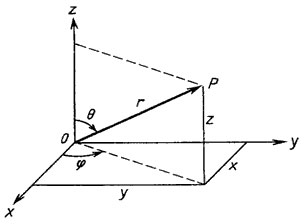
Spherical coordinates.
The position of point M in the spherical coordinate system is determined by a triplet of numbers $r$, $\varphi$, and $\theta$, where:
$r$ is the distance from the origin to point M;
$\varphi$ is the angle formed by the projection of the radius vector onto the xy-plane with the positive direction of the x-axis;
$\theta$ is the angle between the positive direction of the z-axis and the radius vector of point M.
$$\left\{\begin{array}{rcl} x=r\cos\varphi\cos\theta,\\ y=r\sin\varphi\cos\theta,\\ z=r\sin\theta,\end{array}\right.$$
$ (r\geq 0,\;0\leq\varphi \leq 2\pi,\; -\frac{\pi}{2}\le\theta\le\frac{\pi}{2}).$
Generalized polar coordinates.
$$ \left\{\begin{array}{rcl} x=ar\cos^\alpha\varphi\cos^\beta\theta,\\ y=br\sin^\alpha\varphi\cos^\beta\theta,\\ z=cr\sin^\beta\theta, \end{array} \right. $$
$ (r\ge0,\; 0\le \varphi\le 2\pi,\;-\frac{\pi}{2}\le\theta\le\frac{\pi}{2}). $
Tags:
