Geometrical Application of Definite Integral and Application of Riemann Integral in Mechanics and Physics.

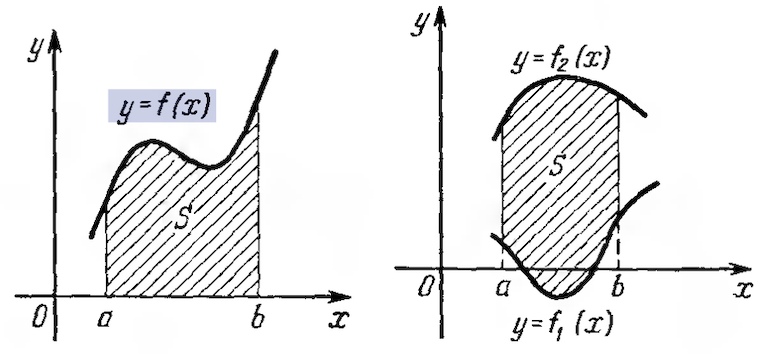
1. The area of a plane figure. The area of a figure bounded by the graph of a continuous function $y=f(x),, (f(x)\geq 0),$ two straight lines $x=a$ and $x=b$ and the $x$-axis, or the area of a curvilinear trapezoid bounded by the arc of the graph of the function $y=f(x),,, a\leq x\leq b$ (see Fig. 1) is calculated by the formula $$S=\int\limits_a^bf(x)dx.$$

The area of a figure bounded by the graphs of continuous functions $y=f_1(x)$ and $y=f_2(x),,, f_1(x)\leq f_2(x)$ and two straight lines $x=a$, $x=b$ (see Fig. 2) is determined by the formula $S=\int\limits_a^b(f_2(x)-f_1(x)),dx$.

If the figure is bounded by a curve with parametric equations $x=x(t),, y=y(t),$ straight lines $x=a,,,x=b$ and the $x$-axis, then its area is calculated by the formula$$S=\int\limits_{t_1}^{t_2}y(t)x'(t)dt=\int\limits_{t_1}^{t_2}y(t)dx(t),\quad (1)$$where the limits of integration are found from the equations $a=x(t_1),,, b=x(t_2),,$($y(t)\geq 0$ on the interval $[t_1,, t_2]$).

Formula (1) is also applicable for calculating the area of a figure bounded by a closed curve (the parameter $t$ should vary from $t_1$ to $t_2$ in a counterclockwise direction).

The area of a figure bounded by the graph of a continuous function $r=r(\varphi)$ and two rays $\varphi=\alpha,$ $\varphi=\beta,$ where $\varphi$ and $r$ are polar coordinates, or the area of a curvilinear sector bounded by the arc of the function graph, $r=r(\varphi),,,\alpha\leq\varphi\leq\beta,$ is calculated by the formula $$S=\frac{1}{2}\int\limits_{\alpha}^{\beta}r^2d\varphi.$$

2. The length of a curve's arc.

If a smooth curve is given by the equation $y=f(x),$ then the length $l$ of its arc is given by the formula $$l=\int\limits_a^b\sqrt{1+(y')^2}\,dx,$$

Where $a$ and $b$ are the abscissas of the ends of the arc.

If the curve is defined by parametric equations $x=x(t),, y=y(t)\quad (t_1\leq t\leq t_2),$ then

$$l=\int\limits_{t_1}^{t_2}\sqrt{(x_t')^2+(y_t')^2}\,dt.$$

Similarly, the length of a curve in space defined by parametric equations $x=x(t),, y=y(t),,, z=z(t),,,t_1\leq t\leq t_2:$ $$l=\int\limits_{t_1}^{t_2}\sqrt{(x_t')^2+(y_t')^2+(z_t')^2}\,dt.$$

If a smooth curve is defined by a polar equation $r=r(\varphi),$ $\alpha\leq\varphi\leq\beta,$ then$$l=\int\limits_{\alpha}^{\beta}\sqrt{r^2+(r')^2}d\varphi.$$

3. Surface area of revolution.

The surface area formed by revolving the arc of a curve, defined by the function $y=f(x),,,a\leq x\leq b,$ around the $x$-axis is calculated by the formula $$Q_x=2\pi\int\limits_a^bf(x)\sqrt{1-(f'(x))^2}\,dx,$$

If the arc is defined by parametric equations $x=x(t),, y=y(t)\quad (t_1\leq t\leq t_2),$ then

$$Q_x=2\pi\int\limits_{t_1}^{t_2}y(t)\sqrt{(x_t')^2+(y_t')^2}\,dt.$$

If the arc is given in polar coordinates as $r=r(\varphi),$ $\alpha\leq\varphi\leq\beta,$ then$$Q_x=2\pi\int\limits_{\alpha}^{\beta}r\sin\varphi\sqrt{r^2+(r')^2}d\varphi.$$

If the arc of the curve rotates around an arbitrary axis, then the surface area of revolution is expressed by an integral. $$Q=2\pi\int\limits_A^BRdl,$$ where $R -$ The distance from a point on the curve to the axis of rotation, $dl$ being the infinitesimal arc length, $A$ and $B$ being the limits of integration corresponding to the ends of the arc. In this case, $R$ and $dl$ should be expressed in terms of the integration variable.

4. Volume of a solid.

If the area $S(x)$ of the cross-section of a solid perpendicular to the $x$-axis is a continuous function on the interval $[a, b]$, then the volume of the solid is calculated by the formula

$$V=\int\limits_a^bS(x)\,dx.$$

The expression for the function $S(x)$ is quite straightforward in the case of bodies of revolution. For example, if a curvilinear trapezoid bounded by the curve $y=f(x),,, a\leq x\leq b$ rotates around the $x$-axis or the $y$-axis, then the volumes of the bodies of revolution are calculated, respectively, by the formulas:

$$V_x=\pi\int\limits_a^bf^2(x)\, dx,$$

$$V_y=2\pi\int\limits_a^b x|f(x)|\,dx,\quad a\geq 0.$$

If a curvilinear sector bounded by the curve $r=r(\varphi)$ and the rays $\varphi=\alpha$ and $\varphi=\beta$ rotates around the polar axis, then the volume of the solid of revolution is equal to $$V=\frac{2}{3}\pi\int_{\alpha}^{\beta}r^3\sin\varphi\,d\varphi.$$

5. Moments and centers of mass of plane curves.

If the arc of a curve is given by the equation $y=f(x), a\leq x\leq b,$ and has a density $\rho=\rho(x),$ then the statistical moments of this arc $M_x$ and $M_y$ with respect to the coordinate axes $Ox$ and $Oy$ are equal to $$M_x=\int\limits_a^b\rho(x)f(x)\sqrt{1+(f'(x))^2}\,dx,$$ $$M_y=\int\limits_a^b\rho(x)x\sqrt{1+(f'(x))^2}\,dx,$$

The moments of inertia $I_x$ and $I_y$ with respect to the same axes $Ox$ and $Oy$ are calculated by the formulas$$I_x=\int\limits_a^b\rho(x)f^2(x)\sqrt{1+(f'(x))^2}\,dx,$$ $$I_y=\int\limits_a^b\rho(x)x^2\sqrt{1+(f'(x))^2}\,dx,$$

and the coordinates of the center of mass $x$ and $y$ by the formulas $$\widetilde{x}=\frac{M_y}{l}=\frac{1}{l}\int\limits_a^b\rho(x)x\sqrt{1+(f'(x))^2}\,dx,$$

$$\widetilde{y}=\frac{M_x}{l}=\frac{1}{l}\int\limits_a^b\rho(x)f(x)\sqrt{1+(f'(x))^2}\,dx,$$

where the mass of the arc, i.e.,

$$I=\int\limits_a^b\rho(x)\sqrt{1+(f'(x))^2}\,dx,$$

6. Physical problems.

The distance traveled by an object with velocity $v(t)$ over the time interval $[t_1, t_2]$ is expressed by the integral$$S=\int\limits_{t_1}^{t_2}v(t)\,dt.$$

The work done by a variable force $f(x)$ acting along the $Ox$ axis over the interval $[a, b]$ is expressed by the integral $$A=\int\limits_a^bf(x)\,dx.$$

Tags: Geometrical Application of Definite Integral, Riemann Integral, Surface area of revolution, The length of a curve's arc, calculus, integral, mathematical analysis