Function analysis using derivatives.
Increasing and Decreasing Functions. Extremum.
A function $y=f(x)$ is called increasing (decreasing) on the interval $(a, b)$ if from the inequality $x_1
If the function $f(x)$ is differentiable on the interval $(a, b)$ and $f'(x)>0$ for all $x\in(a, b),$ then the function $f(x)$ increases on $(a, b);$ if $f'(x)<0$ for all $x\in(a, b),$ then $f(x)$ decreases on this interval.
In simple cases, the domain of definition of the function $y=f(x)$ can be divided into a finite number of monotonicity intervals. Each of the monotonicity intervals is bounded by critical points where $f'(x)=0$ or $f'(x)$ does not exist.
If there exists a neighborhood $U_0(x_0)$ of the point $x_0$ such that for every point $x\neq x_0$ in this neighborhood, the inequality $f(x)>f(x_0)$ (or $f(x)
Necessary condition for an extremum.
If $x_0$ is a point of extremum of the function $f(x),$ then $f'(x_0)=0$ or $f'(x_0)$ does not exist, i.e., $x_0$ is a critical point of this function.
Sufficient conditions for an extremum of a continuous function.
1. Let the function $f(x)$ be differentiable in some neighborhood $(x_0-\delta,,, x_0+\delta)$ of the critical point $x_0,$ except perhaps at this point itself. If in this case, the derivative $f'(x)$ has opposite signs in the intervals $(x_0-\delta,, x_0)$ and $(x_0,, x_0+\delta),$ then $x_0$ is an extremum point. Moreover, if $f'(x)>0$ for $x\in(x_0-\delta, x_0)$ and $f'(x)<0$ for $x\in(x_0, x_0+\delta),$ then $x_0$ is a maximum point, and if $f'(x)<0$ for $x\in(x_0-\delta, x_0)$ and $f'(x)>0$ for $x\in(x_0,, x_0+\delta),$ then $x_0$ is a minimum point. If $f'(x)$ maintains its sign for $x\in(x_0-\delta, x_0+\delta),$ $x\neq x_0,$ then the point $x_0$ is not an extremum point.
2. Let the function $f(x)$ be twice differentiable at the critical point $x_0$ and in some neighborhood of it. If $f''(x_0)<0,$ then $x_0$ is a maximum point of the function $f(x),$ if $f''(x_0)>0,$ then $x_0$ is a minimum point. If $f''(x_0)=0,$ additional investigations are required.
The greatest (smallest) value of a continuous function $f(x)$ on a given interval $[a, b]$ is achieved either at critical points or at the ends of the interval.
Examples:
For the specified functions, find the intervals of increase and decrease and the extremum points.
1. $y=x\sqrt{1-x^2}$
Solution.
Let's find the domain of valid values of the function:
$1-x^2\geq 0\Rightarrow x^2\leq 1\Rightarrow x\in[-1, 1]$
To find the intervals of increase and decrease of the function, let's calculate its derivative and find the intervals where it is of constant sign.
$$y'=x'\sqrt{1-x^2}+x(\sqrt{1-x^2})'=\sqrt{1-x^2}+x\frac{(1-x^2)'}{2\sqrt{1-x^2}}=$$ $$=\sqrt{1-x^2}-\frac{2x^2}{2\sqrt{1-x^2}}=\frac{1-x^2-x^2}{\sqrt{1-x^2}}=\frac{1-2x^2}{\sqrt{1-x^2}}.$$
$$y'=0\Leftrightarrow \frac{1-2x^2}{\sqrt{1-x^2}}=0\Leftrightarrow 1-2x^2=0\Leftrightarrow x^2=\frac{1}{2}\Rightarrow$$ $$\Rightarrow x_1=\frac{1}{\sqrt 2};\,\, x_2=-\frac{1}{\sqrt 2}.$$
$$y'>0\Leftrightarrow \frac{1-2x^2}{\sqrt{1-x^2}}>0\Leftrightarrow 1-2x^2>0\Leftrightarrow x^2<\frac{1}{2}\Rightarrow$$ $$\Rightarrow -\frac{1}{\sqrt 2}
$$y'<0\Leftrightarrow \frac{1-2x^2}{\sqrt{1-x^2}}<0\Rightarrow 1-2x^2<0\Rightarrow x^2>\frac{1}{2}\Rightarrow$$ $$\Rightarrow x\in(-\infty; -\frac{1}{\sqrt 2})\cup (\frac{1}{\sqrt 2},\infty).$$
Given the domain of validity $x\in[-1,-\frac{1}{\sqrt 2})\cup(\frac{1}{\sqrt 2}, 1].$
At the point $x_1=-\frac{1}{\sqrt 2}$, the derivative $y'$ changes sign from $"-"$ to $"+",$ therefore, at this point, the function has a minimum.. $$y_{min}\left(-\frac{1}{\sqrt 2}\right)=-\frac{1}{\sqrt 2}\sqrt{1-\frac{1}{2}}=-\frac{1}{2}.$$ At the point $x_2=\frac{1}{\sqrt 2}$, the derivative $y'$ changes sign from $"+"$ to $"-",$ therefore, at this point, the function has a maximum. $$y_{max}\left(\frac{1}{\sqrt 2}\right)=\frac{1}{\sqrt 2}\sqrt{1-\frac{1}{2}}=\frac{1}{2}.$$
Answer: On $x\in[-1,-\frac{1}{\sqrt 2})\cup(\frac{1}{\sqrt 2}, 1]$, the function decreases; on $x\in(-\frac{1}{\sqrt 2},\frac{1}{\sqrt 2})$, it increases; $y_{min}\left(-\frac{1}{\sqrt 2}\right)=-\frac{1}{2}$; $y_{max}\left(\frac{1}{\sqrt 2}\right)=\frac{1}{2}$.
2.$y=x-2\sin x.$
Solution.
Let's find the domain of valid values of the function:
$x\in(-\infty,, \infty)$
To find the intervals of increase and decrease of the function, let's calculate its derivative and find the intervals where it is of constant sign.
$$y'=x'-2(\sin x)'=1-2\cos x$$
$$y'=0\Rightarrow 1-2\cos x=0\Rightarrow \cos x=\frac{1}{2}\Rightarrow x=\pm\frac{\pi}{3}+2\pi k,\,k\in Z.$$
$$y'>0\Rightarrow 1-2\cos x>0\Rightarrow \cos x<\frac{1}{2}\Rightarrow $$ $$\Rightarrow x\in(\frac{\pi}{3}+2\pi k,\, \frac{5\pi}{3}+ 2\pi k)\,k\in Z.$$
$$y'<0\Rightarrow 1-2\cos x<0\Rightarrow \cos x>\frac{1}{2}\Rightarrow $$ $$\Rightarrow x\in(-\frac{\pi}{3}+2\pi k,\, \frac{\pi}{3}+ 2\pi k)\,k\in Z.$$
At the points $x=\frac{\pi}{3}+2\pi k$, where $k$ is an integer, the derivative $y'$ changes sign from $"-"$ to $"+",$ therefore, at these points, the function has a minimum.
$$y_{min}\left(\frac{\pi}{3}+2\pi k\right)=\frac{\pi}{3}+2\pi k-2\frac{\sqrt 3}{2}.$$ At the points $x=-\frac{\pi}{3}+2\pi k$, where $k$ is an integer, the derivative $y'$ changes sign from $"+"$ to $"-",$ therefore, at these points, the function has a maximum.. $$y_{max}\left(-\frac{\pi}{3}+2\pi k\right)=-\frac{\pi}{3}+2\pi k+2\frac{\sqrt 3}{2}.$$
Answer: On $x\in\left(-\frac{\pi}{3}+2\pi k,, \frac{\pi}{3}+ 2\pi k\right)$, where $k\in \mathbb{Z}$, the function decreases; on $x\in\left(\frac{\pi}{3}+2\pi k,, \frac{5\pi}{3}+ 2\pi k\right)$, where $k\in \mathbb{Z}$, it increases; $y_{min}\left(\frac{\pi}{3}+2\pi k\right)=\frac{\pi}{3}+2\pi k-\sqrt 3$; $y_{max}\left(-\frac{\pi}{3}+2\pi k\right)=-\frac{\pi}{3}+2\pi k+\sqrt 3$.
Determine the maximum and minimum values of the following functions on the specified intervals:
5.413. $y=-3x^4+6x^2;\quad [-2,, 2].$
Solution.
Let's find the extremum points of the given function on the interval $[-2, 2]$ and the value of the function at the endpoints of this interval:
$$y'=-12x^3+12x=12x(-x^2+1)=-12x(x-1)(1+x).$$
$$y'=0\Rightarrow x_1=-1,\,\,\, x_2=0,\,\,\, x_3=1.$$
$$y'>0\Rightarrow y\in (-1, 0)\cup(1,\infty);$$
$$y'<0\Rightarrow y\in (\infty, -1)\cup(0,1).$$
The derivative $y'$ changes sign from $"+"$ to $"-"$ at points $x_1=-1$ and $x_3=1;$ the derivative $y'$ changes sign from $"-"$ to $"+"$ at point $x_2=0.$ Thus, at points $x_1=-1$ and $x_3=1$, the function has a maximum, and at point $x_2=0$, it has a minimum. Let's find the values of the function at all the found extremum points and at the endpoints of the given interval.
$y(-2)=-3\cdot 16+6\cdot 4=-24;$
$y(-1)=-3\cdot 1+6\cdot 1=3;$
$y(0)=0;$
$y(1)=-3\cdot 1+6\cdot 1=3;$
$y(2)=-3\cdot 16+6\cdot 4=-24.$
Choosing the maximum and minimum values, we get the answer.
Answer: $m=y_{min}=-24;,, M=y_{max}=3.$
3. $y=\frac{x-1}{x+1};\quad [0, 4].$
Solution.
Let's write down the domain of validity (ODZ) of the given function:
$$x+1\neq 0\Rightarrow x\neq -1.$$
Let's find the extremum points of the given function on the interval $[0, 4]$ and the value of the function at the endpoints of this interval:
$$y'=\frac{(x-1)'(x+1)-(x+1)'(x-1)}{(x+1)^2}=\frac{x+1-(x-1)}{(x+1)^2}=\frac{2}{(x+1)^2}.$$
It's obvious that $\frac{2}{(x+1)^2}> 0$ for all $x\in[0, 4]$. Therefore, on the entire given interval, $y'> 0$.
Thus, on the interval $[0, 4]$, the function $y(x)$ strictly increases and, therefore, has no extremum points. Let's find the values of the function at the endpoints of the given interval.
$y(0)=\frac{-1}{1}=-1;$
$y(4)=\frac{4-1}{4+1}=\frac{3}{5}=0.6.$
Choosing the maximum and minimum values, we get the answer.
Answer: $m=y_{min}=-1;,, M=y_{max}=0.6.$
To prove the inequalities:
4. $e^x>1+x,\quad x\neq 0.$
Solution.
Let's examine the function $y(x)=e^x-1-x$ for monotonicity:
$y'(x)=e^x-1>0$ when $e^x>1\Rightarrow x>0;$
$y'(x)<0$ when $e^x<1\Rightarrow x<0.$
So, the function $y(x)=e^x-1-x$ increases when $x>0$ and decreases when $x<0.$ Therefore, $x=0$ is a minimum point. Since at $x=0$ we have $y(0)=e^0-1-0=0$, for all other values $y(x)=e^x-1-x>0,\Rightarrow, e^x>1+x.$
Which proves the statement.
5. $\sin x+\tan x>2x,\quad x\in (0, \frac{\pi}{2}).$
Solution.
Let's examine the function $y(x)=\sin x+\tan x-2x$ for monotonicity:
$$y'(x)=\cos x+\frac{1}{\cos^2x}-2=\frac{\cos^3x-2\cos^2 x+1}{\cos^2 x}=\frac{\cos^2 x(\cos x-2)+1}{\cos^2 x}=$$ $$=\frac{\cos^2(-2\sin^2\frac{x}{2}-1)+\cos^2 x+\sin^2 x}{\cos^2 x}=$$ $$=\frac{\cos^2 x(-2\sin^2\frac{x}{2})+\sin^2 x}{\cos^2 x}=\frac{-2\cos^2x\sin^2\frac{x}{2}+4\sin^2\frac{x}{2}\cos^2\frac{x}{2}}{\cos^2 x}=$$ $$=\frac{2\sin^2\frac{x}{2}}{\cos^2\frac{x}{2}}\left(-\cos^2x+2\cos^2\frac{x}{2}\right)=$$ $$=\frac{2\sin^2\frac{x}{2}}{\cos^2\frac{x}{2}}\left(-\left(2\cos^2\frac{x}{2}-1\right)+2\cos^2\frac{x}{2}\right)=\frac{2\sin^2\frac{x}{2}}{\cos^2\frac{x}{2}}>0.$$
So, the function $y(x)=\sin x+\tan x-2x$ increases over its entire domain, particularly when $x\in(0, \frac{\pi}{2}).$ Since at $x=0$, $y(0)=\sin 0+ \tan 0-2\cdot 0=0,$ and the function is continuous for $x\in(0, \frac{\pi}{2})$, then $y(x)=\sin x+\tan x-2x>0\Rightarrow \sin x+\tan x> 2x$ for $x\in(0, \frac{\pi}{2}).$
Which proves the statement.
6. Determine the largest area of a rectangle inscribed in a circle of radius $r.$
Solution.
Let the angles between the diagonals of the rectangle be $2\varphi$ and $\pi-2\varphi$ $(\varphi\in(0, \frac{\pi}{2})).$ Then the lengths of the sides are $r\sin\varphi$ and $r\cos\varphi.$ Accordingly, the area of the rectangle is
$$S=S(\varphi)=r\sin\varphi\cdot r\cos\varphi=\frac{1}{2}r^2\sin 2\varphi.$$
Let's find the maximum area, we will determine the maximum of the function $S(\varphi):$ $$S'(\varphi)=\frac{1}{2}r^2 2\cos 2\varphi=r^2\cos 2\varphi.$$ $$S'(\varphi)=0\Rightarrow r^2\cos 2\varphi=0\Rightarrow 2\varphi=\pi/2\Rightarrow \varphi=\pi/4.$$
In this case $$S'(\varphi)<0\Rightarrow r^2\cos 2\varphi<0\Rightarrow 2\varphi=\in(\pi/2; \pi)\Rightarrow \varphi\in(\pi/4;\pi/2)$$ $$S'(\varphi)>0\Rightarrow r^2\cos 2\varphi>\Rightarrow 2\varphi\in(0,\pi/2)\Rightarrow \varphi\in(0, \pi/4).$$
Therefore, when $\varphi=\frac{\pi}{4}$, the function $S(\varphi)$ reaches its maximum.
$$S(\pi/4)=\frac{1}{2}r^2\sin \left(2\frac{\pi}{4}\right)=\frac{1}{2}r^2\sin\frac{\pi}{2}=\frac{r^2}{2}.$$
Answer: $\frac{r^2}{2}.$
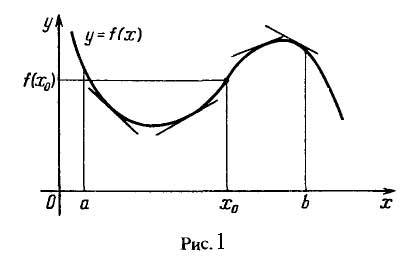
The graph of a differentiable function $y=f(x)$ is said to be concave downward (or convex upward) on the interval $(a, b)$ if the curve on this interval lies above the tangent drawn to the graph of the function $y=f(x)$ at any point $x\in (a, b)$.
If, on the interval $(a, b)$, every tangent lies above the curve of the function, then the graph of the differentiable function on this interval is called concave upward (or convex downward) (on Fig. 1, the graph of the function $y=f(x)$ is concave downward on the interval $(a, x_0)$ and convex upward on the interval $(x_0, b)$).
If a function is twice differentiable on $(a, b)$ and $f''(x)>0$ ($f''(x)<0$), then its graph is concave downward (upward) on this interval.
In simple cases, the domain of the function $f(x)$ can be divided into a finite number of intervals with a constant direction of concavity. Each of these intervals is bounded by points where $f''(x)=0$ or $f''(x)$ does not exist. The point $(x_0, f(x_0))$ where the direction of concavity of the graph of the function changes to the opposite is called an inflection point (see Fig. 1).
Sufficient condition for an inflection point:
Let the function $f(x)$ be twice differentiable in some neighborhood $U_0(x_0)$ of the point $x_0$ where $f''(x_0)=0$ or $f''(x_0)$ does not exist. If, in the intervals $(x_0-\delta, x_0)$ and $(x_0, x_0+\delta)$, the derivative $f''(x)$ has opposite signs, then $x_0$ is an inflection point.
Examples:
Find the intervals of concavity of the graph of the function, inflection points, and the slopes of the tangents at the inflection points:
7 $y=x^7+7x+1.$
Solution.
To find the intervals of concavity of the function, let's find its second derivative and investigate its sign:
$$y''=(x^7+7x+1)''=(7x^6+7)'=42x^5.$$
$y''=0\Rightarrow x=0;$
$y''>0\Rightarrow x>0;$
$y''<0\Rightarrow x<0.$
Thus, for $x\in(0, +\infty)$, the function $y(x)$ is concave downward, for $x\in(-\infty, 0)$, the function $y(x)$ is concave upward, and the point with coordinates $x=0$ is an inflection point.
$y(0)=1.$ Therefore, the inflection point is $(0, 1).$
Let's find the slope of the tangent at the inflection point:
$k=y'(0)=7.$
Answer: For $x\in(0, +\infty)$, the function $y(x)$ is concave downward, for $x\in(-\infty, 0)$, the function $y(x)$ is concave upward, $(0, 1)$ is the inflection point; $k=y'(0)=7.$
8. $y=\sqrt[3]{(x+1)^2}+\sqrt[3]{(x-1)^2}.$
Solution.
Let's find the second derivative of the function $y(x)$ and investigate its sign:
$$y''=(\sqrt[3]{(x+1)^2}+\sqrt[3]{(x-1)^2})''=\left(\frac{2}{3}(x+1)^{-\frac{1}{3}}+\frac{2}{3}(x-1)^{-\frac{1}{3}}\right)'=$$ $$=-\frac{2}{9}(x+1)^{-\frac{4}{3}}-\frac{2}{9}(x-1)^{-\frac{4}{3}}=-\frac{2}{9}\left((x+1)^{-4/3}+(x-1)^{-4/3}\right).$$
$y''<0$ for the entire domain. Therefore, the graph is concave upward everywhere.
Answer: The graph is concave upward everywhere.
9. $y=x^3\ln x+1.$
Solution.
Let's find the second derivative of the function $y(x)$ and investigate its sign:
$$y''=(3x^2\ln x+x^2)'=6x\ln x+3x+2x=6x\ln x+5x=x(6\ln x+5).$$
$y''=0\Rightarrow x_1=0;\,\, x_2=e^{-5/6}$
$y''>0\Rightarrow x>e^{-5/6};$
$y''<0\Rightarrow x\in(0, e^{-5/6}).$
Thus, for $x\in(e^{-5/6}, +\infty)$, the function $y(x)$ is concave downward, for $x\in(0, e^{-5/6})$, the function $y(x)$ is concave upward, and the point with coordinates $x=e^{-5/6}$ is an inflection point.
$y(e^{-5/6})=e^{-15/6}\ln e^{-5/6}+1=-\frac{5}{6}e^{-5/2}+1.$ Therefore, the inflection point is $\left(e^{-5/6}, -\frac{5}{6}e^{-15/6}+1\right).$
Let's find the slope of the tangent at the inflection point:
$k=y'(e^{-5/6})=3e^{-10/6}\ln e^{-5/6}+e^{-10/6}=-\frac{15}{6}3e^{-5/3}+e^{-5/3}=-1.5e^{-5/3}.$
Answer: For $x\in(e^{-5/6}, +\infty)$, the function $y(x)$ is concave downward, for $x\in(0, e^{-5/6})$, the function $y(x)$ is concave upward, the inflection point is at $\left(e^{-5/6}, 1-\frac{5}{6}e^{-15/6}\right)$; $k=y'(0)=-1.5e^{-5/3}.$ Tags:
Convexity Direction,
Extremum,
Function analysis,
Increasing and Decreasing Functions,
Points of Inflection,
Sufficient conditions for extremum,
calculus,
derivative,
derivative table,
mathematical analysis
Convexity Direction. Points of Inflection.