Computing double integrals

Definition: The double integral of a continuous function $f(x, y)$ over a bounded closed and squareable region $\Omega$ is defined as the number$$\iint\limits_{\Omega}f(x,y)dxdy=\lim\limits_{max|\Delta x_i|\rightarrow 0\quad max|\Delta y_i|\rightarrow 0}\sum\limits_i\sum\limits_j f(x_i, y_j)\Delta x_i\Delta y_j ,$$ where $\Delta x_i = x_{i+1} - x_i$, $\Delta y_j = y_{j+1} - y_j$, and the sum extends over those values of $i$ and $j$ for which $(x_i, y_j) \in \Omega$.

Direct computation of the double integral.

If the region $\Omega$ is defined by the inequalities $$a\leq x\leq b,\qquad y_1(x)\leq y\leq y_2 (x),$$ where $y_1(x)$ and $y_2(x)$ are continuous functions on the interval $[a, b]$, then the corresponding double integral can be computed using the formula $$\iint\limits_{\Omega}f(x, y)dxdy=\int\limits_a^bdx\int\limits_{y_1(x)}^{y_2(x)}f(x, y)dy.$$

Change of variables in a double integral.

If continuously differentiable functions $$x=x(u, v),\quad y=y(u, v)$$ provide a one-to-one mapping of the bounded and closed region $\Omega$ in the plane $Oxy$ onto the region $\Omega'$ in the plane $Ouv$, and the Jacobian $$I=\frac{D(x, y)}{D(u, v)}$$ maintains a constant sign in $\Omega$ except perhaps on a set of measure zero, then the formula holds true:$$\iint\limits_{\Omega}f(x, y)dxdy=\iint\limits_{\Omega'}f(x(u, v), y(u, v))|I|dudv.$$

In particular, for the case of transitioning to polar coordinates $r$ and $\varphi$, the formula becomes:$$\iint\limits_{\Omega}f(x, y)dxdy=\iint\limits_{\Omega'}f(r\cos\varphi,\, r\sin\varphi)r drd\varphi.$$

Examples:

Compute the integrals.

1. $\int\limits_0^1dx\int\limits_0^1(x+y)dy.$

Solution.

$$\int\limits_0^1dx\int\limits_0^1(x+y)dy=\int\limits_0^1\left(\left.\left(xy+\frac{y^2}{2}\right)\right|_0^1\right)dx=$$ $$=\int\limits_0^1\left(x+\frac{1}{2}-0\right)dx=\left.\left(\frac{x^2}{2}+ \frac{1}{2}x\right)\right|_0^1= \frac{1}{2}+\frac{1}{2}-0=1.$$

Answer: 1.

2. $\int\limits_0^{2\pi}d\varphi\int\limits_0^ar^2\sin^2\varphi\,dr.$

Solution.

$$\int\limits_0^{2\pi}d\varphi\int\limits_0^ar^2\sin^2\varphi\,dr=\int\limits_0^{2\pi}\left(\int\limits_0^a r^2\sin^2\varphi\,dr\right)d\varphi=$$ $$=\int\limits_0^{2\pi}\left(\sin^2\varphi\left.\frac{r^3}{3}\right|_0^a\right)d\varphi=\int\limits_0^{2\pi}\sin^2\varphi\left(\frac{a^3}{3}-0\right)d\varphi=$$

$$=\frac{a^3}{3}\int\limits_0^{2\pi}\frac{1-cos2\varphi}{2}d\varphi=\frac{a^3}{3}\left.\left(\frac{1}{2}\varphi-\frac{1}{4}\sin2\varphi\right)\right|_0^{2\pi}=$$ $$=\frac{a^3}{3}\left(\frac{1}{2}2\pi-\frac{1}{4}\sin4\varphi-0\right)=\frac{a^3\pi}{3}.$$

Answer: $\frac{a^3\pi}{3}.$

3. What sign does the integral $\iint\limits_{|x|+|y|\leq 1}\ln(x^2+y^2),dxdy$ have?

Change the order of integration in the following integrals:

4. $\int\limits_0^2dx\int\limits_x^{2x}f(x, y)dy.$

Solution:

Let's draw the region of integration:

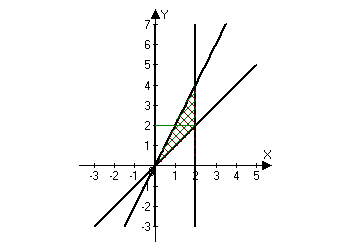
The region of integration is bounded by the lines $y=x$, $y=2x$, and $x=2$. Note that in this region, if $y$ varies from $0$ to $2$, then the coordinate $x$ varies from the line $y=2x$ (or $x=\frac{y}{2}$) to $y=x$. If $y$ varies from $2$ to $4$, then the coordinate $x$ varies from the line $y=2x$ ($x=\frac{y}{2}$) to $x=2$. Thus,

$$\int\limits_0^2dx\int\limits_x^{2x}f(x, y)dy=\int\limits_0^2dy\int\limits_{\frac{y}{2}}^xdx+\int\limits_2^4dy\int\limits_{\frac{y}{2}}^{2}dx.$$

Answer: $\int\limits_0^2dx\int\limits_x^{2x}f(x, y)dy=\int\limits_0^2dy\int\limits_{\frac{y}{2}}^xdx+\int\limits_2^4dy\int\limits_{\frac{y}{2}}^{2}dx.$

1. $\int\limits_1^2dx\int\limits_{2-x}^{\sqrt{2x-x^2}}f(x, y)dy.$

2. Evaluate the integral $\iint\limits_{\Omega}xy^2dxdy$ if the region $\Omega$ is bounded by the parabola $y^2=2px$ and the line $x=p/2\quad (p>0).$

3. In the double integral $\iint\limits_{\Omega}f(x,y)dxdy$, switch to polar coordinates $r$ and $\varphi$, where $x=r\cos\varphi$ and $y=r\sin\varphi$. Establish the limits of integration if $\Omega$ is a ring $a^2\leq x^2+y^2\leq b^2.$

4. Switch to polar coordinates, $r$ and $\varphi$, where $x=r\cos\varphi$ and $y=r\sin\varphi$, and establish the limits of integration in both orders in the following integral: $\int\limits_0^1dx\int\limits_{1-x}^{\sqrt{1-x^2}}f(x, y)dy.$

5. Assuming $r$ and $\varphi$ are polar coordinates, change the order of integration in the following integrals: $\int\limits_{-\pi/2}^{\pi/2}d\varphi\int\limits_0^{a\cos\varphi}f(\varphi,r)dt\quad (a>0).$

6. Switching to polar coordinates, compute the double integral $\iint\limits_{x^2+y^2\leq a^2}\sqrt{x^2+y^2}dxdy.$

7. Instead of $x$ and $y$, introduce new variables $u$ and $v$ and define the limits of integration in the following double integrals $\int\limits_0^2dx\int\limits_{1-x}^{2-x}f(x, y)dy$, where $u=x+y,,, v=x-y.$

8. By making appropriate variable substitutions, reduce the double integrals to single integrals:

$\iint\limits_{\Omega}f(xy)dxdy$, where the region $\Omega$ is bounded by the curves $xy=1,,, xy=2,,, y=x,,, y=4x,, (x>0, y>0).$

Tags: