From Direction to Dimensions: Mastering Vectors in Data Science

Vectors are a cornerstone in the world of data science, forming the backbone of many mathematical concepts used in machine learning, computer vision, and other fields. Let's dive into what vectors are, their properties, and how they help data scientists.

What is a Vector?

A vector is a mathematical entity that has both magnitude and direction. It is often represented as an ordered tuple of numbers in a coordinate system. For example, a 2D vector can be written as:

$a = (x_1, x_2)$

This vector can be visualized as an arrow in a 2D plane, pointing from the origin $(0, 0)$ to the point $(x_1, x_2)$.

In higher dimensions, such as 3D or $n$-dimensional space, a vector extends this idea:

$b = (x_1, x_2, x_3, \dots, x_n)$

Vector Operations

Vectors can be manipulated using various operations, each with practical applications in data science.

1. Addition
   The sum of two vectors, $a$ and $b$, is calculated component-wise:

   $a + b = (a_1 + b_1, a_2 + b_2)$

2. Scalar Multiplication
   Multiplying a vector by a scalar $k$ scales its magnitude without changing its direction:

   $k a = (k \cdot a_1, k \cdot a_2)$

3. Dot Product
   The dot product measures the similarity between two vectors:

   $a \cdot b = \sum_{i=1}^{n} a_i b_i$

   If the dot product is zero, the vectors are orthogonal (perpendicular).

4. Magnitude (Norm)
   The magnitude of a vector measures its length:

   $|a| = \sqrt{a_1^2 + a_2^2 + \dots + a_n^2}$

Vectors in Data Science

Vectors are foundational for representing data. In machine learning:

• Feature vectors are used to encode data points, where each dimension corresponds to a feature.
• Gradient vectors help optimize functions, such as finding minima during model training.
• Word embeddings, like those in natural language processing, are vector representations of words that capture their meaning.

For example, consider a dataset of houses. Each house can be represented as a vector:

$h = (\text{size}, \text{price}, \text{bedrooms}, \text{location})$

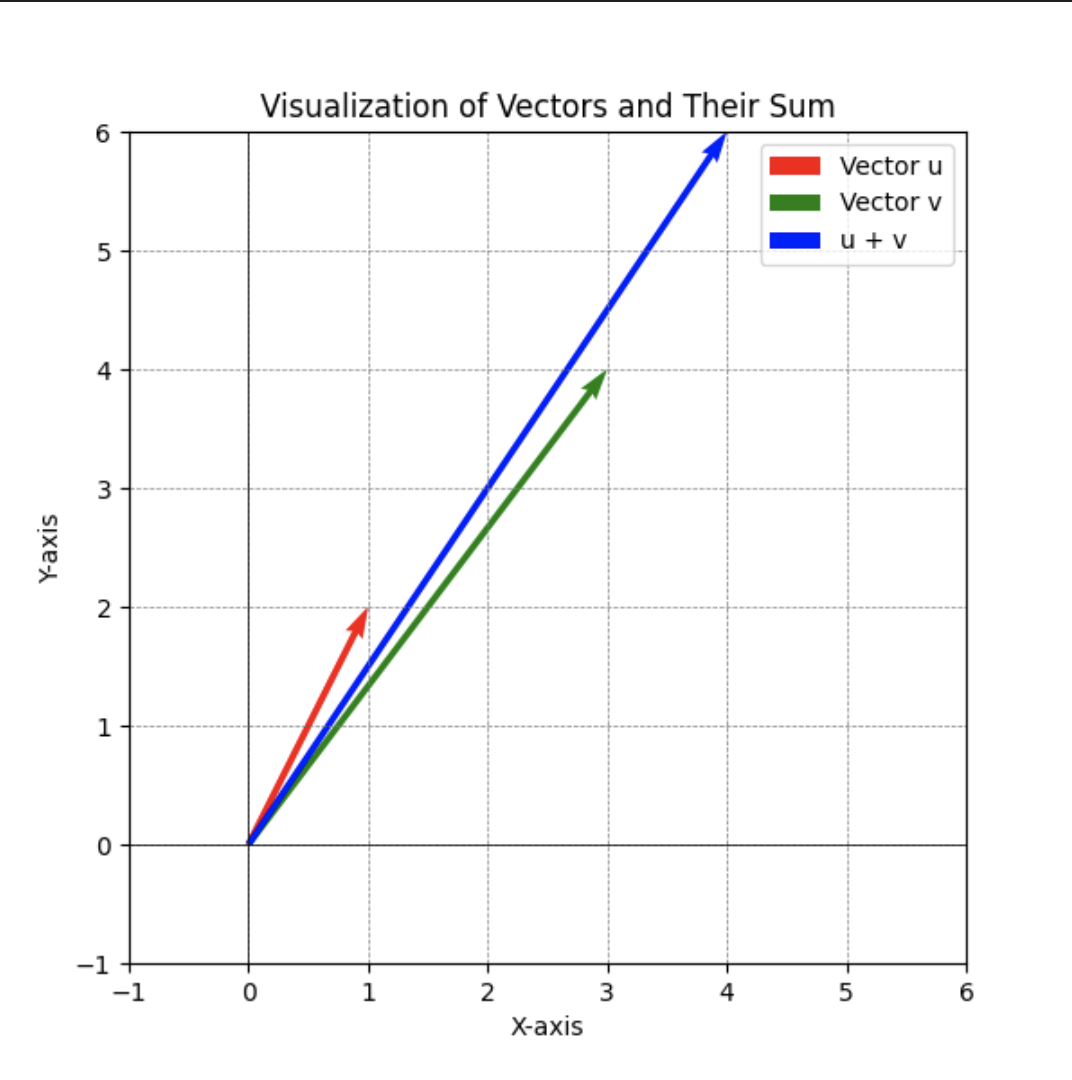
Visualizing Vectors

In 2D and 3D, vectors are arrows. Tools like Matplotlib in Python can help plot these visualizations, making concepts like addition or orthogonality clearer.

For example, if you have two vectors:

$u = (1, 2), v = (3, 4)$

You can visualize their sum as:

$u + v = (4, 6)$

import matplotlib.pyplot as plt
import numpy as np

# Define the vectors
u = np.array([1, 2])
v = np.array([3, 4])
sum_vector = u + v

# Set up the plot
plt.figure(figsize=(6, 6))
plt.quiver(0, 0, u[0], u[1], angles='xy', scale_units='xy', scale=1, color='r', label='Vector u')
plt.quiver(0, 0, v[0], v[1], angles='xy', scale_units='xy', scale=1, color='g', label='Vector v')
plt.quiver(0, 0, sum_vector[0], sum_vector[1], angles='xy', scale_units='xy', scale=1, color='b', label='u + v')

# Add labels and grid
plt.xlim(-1, 6)
plt.ylim(-1, 6)
plt.axhline(0, color='black',linewidth=0.5)
plt.axvline(0, color='black',linewidth=0.5)
plt.grid(color = 'gray', linestyle = '--', linewidth = 0.5)
plt.legend()
plt.title('Visualization of Vectors and Their Sum')
plt.xlabel('X-axis')
plt.ylabel('Y-axis')

# Show the plot
plt.show()

Conclusion

Understanding vectors is crucial for any aspiring data scientist. They provide a compact, powerful way to represent and manipulate data, enabling advanced mathematical techniques like Principal Component Analysis (PCA) and deep learning.

Tags: vectors, data science, machine learning, vector math, linear algebra, vector operations, feature vectors

Tags: Data Science, Feature Vectors, Linear Algebra, Machine Learning, Vector Math, Vector Operations, Vectors