The plane in space, various equations, the distance from a point to a plane.

Literature: Collection of problems in mathematics. Part 1. Edited by A. V. Efimov, B. P. Demidovich.

There are such forms of writing the equation of a plane:

1) $Ax+By+Cz+D=0 -$ the general equation of the plane $P,$ where $\overline{N}=(A, B, C) -$ the normal vector of the plane $P.$

2) $A(x-x_0)+B(y-y_0)+C(z-z_0)=0 -$ the equation of the plane $P,$ which passes through the point $M(x_0, y_0, z_0)$ perpendicular to the vector $\overline{N}=(A, B, C).$ The vector $\overline N$ is called the normal vector of the plane.

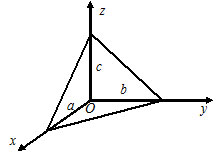
3) $\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1 -$ the equation of the plane in intercepts on the axes, where $a,$ $b,$ and $c -$ the lengths of the segments that the plane cuts off on the coordinate axes.

4) $$\begin{vmatrix}x-x_1&y-y_1&z-z_1\\x_2-x_1&y_2-y_1&z_2-z_1\\x_3-x_1&x_2-x_1&x_3-x_1\end{vmatrix}=0 $$ - the equation of the plane, which passes through three points $A(x_1, y_1, z_1), B(x_2, y_2, z_2),$ and $C(x_3, y_3, z_3).$

5) $x\cos\alpha+y\cos\beta+z\cos\gamma-p=0 -$ the normal equation of the plane, where $\cos\alpha, \cos\beta,$ and $\cos\gamma -$ the directional cosines of the normal vector $\overline{N},$ directed from the origin towards the plane, and $p>0 -$ the distance from the origin to the plane.

The general equation of the plane is converted to the normal form by multiplying by the normalizing factor $\mu=-\frac{sgn D}{\sqrt{A^2+B^2+C^2}}.$

The distance from the point $M(x_0, y_0, z_0)$ to the plane $P: Ax+By+Cz+D=0$ is calculated using the formula. $$d=\left|\frac{Ax_0+By_0+Cz_0+D}{\sqrt{A^2+B^2+C^2}}\right|.$$

Examples:

2.180.

a) Given the plane $P: -2x+y-z+1=0$ and the point $M(1, 1, 1).$ Write the equation of the plane $P',$ passing through the point $M$ parallel to the plane $P$ and calculate the distance $\rho(P, P').$

Solution.

Since the planes $P$ and $P'$ are parallel, the normal vector for the plane $P$ will also be the normal vector for the plane $P'.$ From the equation of the plane, we get $\overline{N}=(-2, 1, -1).$

Next, we write the equation of the plane using the formula (2): $A(x-x_0)+B(y-y_0)+C(z-z_0)=0 -$ the equation of the plane that passes through the point $M(x_0, y_0, z_0)$ perpendicular to the vector $\overline{N}=(A, B, C).$

$-2(x-1)+(y-1)-(z-1)=0\Rightarrow -2x+y-z+2=0.$

Answer: $-2x+y-z+2=0.$

2.181.

a) Write the equation of the plane $P',$ passing through the given points $M_1(1, 2, 0)$ and $M_2(2, 1, 1)$ perpendicular to the given plane $P: -x+y-1=0.$

Solution.

From the equation of the plane $P,$ we find its normal vector $\overline{N}=(-1, 1, 0).$ A plane perpendicular to plane $P$ is parallel to its normal vector. It follows that we can choose a point $M_3(x, y, z) \in P'$ such that $\overline{M_1M_3} || \overline{N}.$

$\overline{M_1M_3}=(x-1, y-2, z).$

The condition for the collinearity of vectors $\overline{M_1M_3}$ and $\overline{N}:$ $\frac{x_{M_1M_3}}{x_N}=\frac{y_{M_1M_3}}{y_N}=\frac{z_{M_1M_3}}{z_N}.$

Since $z_N=0,$ i.e., the vector $N$ lies in the $XoY$ plane, $z_{M_1M_3}=0.$

$\frac{x-1}{-1}=\frac{y-2}{1}.$ Let $x=2,$ then $y=1.$

We found the point $M_3=(2, 1, 0).$

Since point $M_1 \in P',$ then $M_3 \in P'$ as well. Write the equation of the plane passing through three points $M_1 (1, 2, 0),$ $M_2(2, 1, 1),$ and $M_3(2, 1, 0).$

$\begin{vmatrix}x-1&y-2&z\\1&-1&1\\1&-1&0\end{vmatrix}=0 \Rightarrow$

$(x-1)(-1)0+(-1)z+(y-2)-(-1)z-(-1)(x-1)-(y-2)0=0\Rightarrow$ $\Rightarrow -z+y-2+z+x-1=0\Rightarrow x+y-3=0.$

Answer: $x+y-3=0.$

2.182.

a) Write the equation of the plane $P,$ passing through the point $M(1, 1, 1)$ parallel to vectors $a_1(0, 1, 2)$ and $a_2(-1, 0, 1).$

Solution.

Since the vector $[a_1, a_2]$ is perpendicular to the plane of vectors $a_1$ and $a_2$ (see vector product), it will also be perpendicular to the desired plane. Thus, the vector $[a_1, a_2]$ is normal to the plane $P.$ Let's find this vector:

$[a_1, a_2]=\begin{vmatrix}i&j&k\\0&1&2\\-1&0&1\end{vmatrix}=i(1-0)-j(0+2)+k(0+1)=i-2j+k.$

Hence, $\overline{N}=[a_1, a_2]=(1, -2, 1).$

Now we can find the equation of the plane $P,$ using the formula (2), as the plane passing through the point $M(1, 1, 1)$ perpendicular to the vector $\overline N=(1, -2, 1):$

$1(x-1)-2(y-1)+1(z-1)=0\Rightarrow$

$x-2y+z=0.$

Answer: $x-2y+z=0.$

2.183.

a) Write the equation of the plane $P,$ passing through points $M_1(1, 2, 0)$ and $M_2(2, 1, 1)$ parallel to the vector $a=(3, 0, 1).$

Solution.

Since the vector $a$ is parallel to the plane $P,$ for any vector $\overline{M_1M_3},$ parallel to vector $a,$ the point $M_3$ lies in $P.$

Let $M_3=(x, y, z).$ Then $\overline{M_1M_3}=(x-1, y-2, z).$ As $\overline{M_1M_3}\parallel a,$ we have $\frac{x_{M_1M_3}}{x_a}=\frac{y_{M_1M_3}}{y_a}=\frac{z_{M_1M_3}}{z_a}.$ Since $y_a=0,$ vector $a$ lies in the $XoZ$ plane, and any vector parallel to it will also lie in this plane. Hence, $y_{M_1M_3}=y-2=0\Rightarrow y=2.$

From the condition of parallelism of vectors, we have $\frac{x-1}{3}=\frac{z}{1}.$ Let's take $x=4,$ then $z=1.$

We have found the point $M_3=(4, 2, 1).$

Now, write the equation of the plane passing through three points $M_1 (1, 2, 0), M_2(2, 1, 1),$ and $M_3(4, 2, 1).$

$\begin{vmatrix}x-1&y-2&z\\1&-1&1\\3&0&1\end{vmatrix}=0 \Rightarrow$

$(x-1)(-1)1+1\cdot z\cdot 0+(y-2)3-3(-1)z-0\cdot 1\cdot(x-1)-1(y-2)1=0\Rightarrow$

$-x+1+3y-6+3z-y+2=0\Rightarrow -x+2y+3z-3=0.$

Answer: $-x+2y+3z-3=0.$

2.184.

a) Write the equation of the plane passing through three given points $M_1(1, 2,0),$ $M_2(2, 1, 1)$ and $M_3(3, 0, 1).$

Solution.

Let's use formula (4):

$\begin{vmatrix}x-1&y-2&z\\2-1&1-2&1\\3-1&0-2&1\end{vmatrix}=0 \Rightarrow$

$\begin{vmatrix}x-1&y-2&z\\1&-1&1\\2&-2&1\end{vmatrix}=0 \Rightarrow$

$(x-1)(-1) \cdot 1 + z(-2) + 2(y-2) \cdot 1 - 2(-1)z - (-2)(x-1) - 1(y-2) \cdot 1 = 0 \Rightarrow$

$\Rightarrow -x+1 - 2z + 2y - 4 + 2z + 2x - 2 - y + 2 = 0 \Rightarrow x + y - 3 = 0.$

Answer: $x + y - 3 = 0.$