The geometric interpretation of complex numbers.

The set of real numbers can be regarded as a subset of complex numbers where $Im z = 0$.

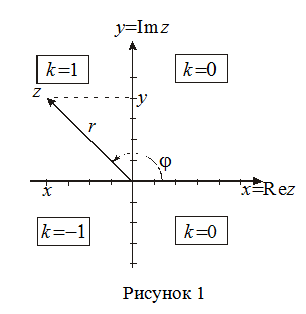
Complex number $z = x + iy$ is represented on the coordinate plane $Oxy$ by a point with coordinates $(x; y)$. This plane is called the complex plane $C$ (see figure 1), where the $Ox$ axis is called the real axis, and the $Oy$ axis is called the imaginary axis. Thus, a real number $z = x + 0i = x$ corresponds to a point on the real axis, and an imaginary number $z = 0 + iy = iy$ corresponds to a point on the imaginary axis.

It is also possible to represent a complex number in the form of a radius-vector ${x, y}$ and define it by specifying its length $r$ and angle $\varphi$ between the $Ox$ axis and the vector.

The length of this vector is called the modulus of the complex number $$|z|=r=\sqrt{x^2+y^2}\geq 0,$$ and the angle $\varphi$ is called the argument of the complex number, denoted by $Arg z$. The argument is determined up to the term $2\pi k$ $(k = 0, \pm 1, \pm 2, \pm 3, ...)$ and for positive values, it is measured counterclockwise from the $Ox$ axis to the vector, while for negative values, it is measured clockwise.

The value of the argument belonging to the interval $(-\pi, \pi]$ is called the principal value of the argument and is denoted $arg z$. The principal value of the argument for the number $x + iy$ can be computed by the formula $\varphi = \arg z = \arctan\left(\frac{y}{x}\right) + k\pi$, where $k = 0$ if $z$ lies in the first or fourth quadrants, $k = 1$ if $z$ lies in the second quadrant, $k = -1$ if $z$ lies in the third quadrant. If $x = Rez = 0$, then $\varphi = \pi/2$ when $y = Imz > 0$ and $\varphi = -\pi/2$ when $y = Imz < 0$.