The Euler and de Moivre's formulas. The nth root of a complex number.
Literature: Collection of problems in mathematics. Part 1. Edited by A. V. Efimov, B. P. Demidovich.
Euler's formulas:
$$\cos\varphi=\frac{e^{i\varphi}+e^{-i\varphi}}{2}; \qquad\qquad \sin\varphi=\frac{e^{i\varphi}-e^{-i\varphi}}{2i}$$
De Moivre's formula
If $z=re^{i\varphi}$, then $$z^n=r^ne^{in\varphi},$$or, in trigonometric form:
$$z^n=r^n(\cos n\varphi+i\sin n\varphi).$$
Let $a=re^{i\varphi}$, $a\neq 0$, be a fixed complex number. Then the equation $z^n=a$, $n\in \mathbb{N}$, has exactly $n$ distinct solutions $z_0, z_1, ..., z_{n-1}$, and these solutions are given by the formula $$z_k=\sqrt[n]{r}e^{i\left(\frac{\varphi}{n}+\frac{2\pi}{n}k\right)}=\sqrt[n]{r}\left(\cos\frac{\varphi+2\pi k}{n}+i\sin\frac{\varphi+2\pi k}{n}\right),$$ $$k=0, 1, ... , n-1.$$(Here $\sqrt{r}$ is a real positive number) The numbers $z_k$, $k=0, 1, ..., n-1$, are called the $n$th roots of the complex number $a$ and are denoted by the symbol $\sqrt[n]{a}$.
Examples:
1.483. Prove Euler's formula $\cos\varphi=\frac{e^{i\varphi}+e^{-i\varphi}}{2}$.
Solution.
It is known that $e^{i\varphi}=\cos{\varphi}+i\sin\varphi$. Accordingly, $e^{-i\varphi}=\cos{(-\varphi)}+i\sin(-\varphi)=\cos\varphi-i\sin\varphi$.
From this, we find $e^{i\varphi}+e^{-i\varphi}=\cos\varphi+i\sin\varphi+\cos\varphi-i\sin\varphi=2\cos\varphi$.
Therefore, $\cos\varphi=\frac{e^{i\varphi}+e^{-i\varphi}}{2}$. This is what needed to be proven.
Using de Moivre's formula, compute the following expressions:
1.485. $(1+i)^{10}$.
Solution.
Let's express the number $z=1+i$ in exponential form:
$r=\sqrt{x^2+y^2}=\sqrt{1+1}=\sqrt{2}$.
Since the number $z$ lies in the first quadrant, we have:
$\tan\varphi=\frac{y}{x}=\frac{1}{1}=1$. And $\varphi=\frac{\pi}{4}$.
Thus, we can express the number $z=1+i$ in exponential form: $z=\sqrt{2} e^{i\frac{\pi}{4}}$.
Now, using de Moivre's formula, we can find $z^{10}$:
$$(1+i)^{10}=(\sqrt 2 e^{i\frac{\pi}{4}})^{10}=(\sqrt 2)^{10}e^{i\frac{10\pi}{4}}=$$
$$=32e^{i\frac{5\pi}{2}}=32(\cos\frac{5\pi}{2}+i\sin{5\pi}{2})=32i.$$
Answer: $(1+i)^{10}=32i.$
1.491. Using de Moivre's formula, express the function $\cos 3\varphi$ in terms of $\cos\varphi$ and $\sin\varphi$.
Solution.
$$\cos 3\varphi=\frac{e^{3i\varphi}+e^{-3i\varphi}}{2}=\frac{1}{2}\left((\cos\varphi+i\sin\varphi)^3+(\cos(-\varphi)+i\sin(-\varphi))^3\right)=$$
$$=\frac{1}{2}\left(\cos^3\varphi+3i\cos^2\varphi\sin\varphi+3i^2\cos\varphi\sin^2\varphi+i^3\sin^3\varphi \right. +$$
$$+\left.\cos^3(-\varphi)-3i\cos^2(-\varphi)\sin(-\varphi)+3i^2\cos(-\varphi)\sin^2(-\varphi)-i^3\sin^3(-\varphi)\right)=$$ $$=\frac{1}{2}\left(\cos^3{\varphi}+3i(1-\sin^2\varphi)\sin\varphi-3\cos\varphi(1-\cos^2\varphi)\right.-i\sin^3\varphi+$$ $$+\left.\cos^3\varphi+3i(1-\sin^2\varphi)\sin\varphi-3\cos\varphi(1-\cos^2\varphi)-i\sin^3\varphi\right)=$$ $$=\cos^3\varphi+3i\sin\varphi-3i\sin^3\varphi-3\cos\varphi+3\cos^3\varphi-i\sin^3\varphi=$$ $$=4\cos^3\varphi-3\cos\varphi+3i\sin\varphi-4i\sin^3\varphi.$$
Answer: $4\cos^3\varphi-3\cos\varphi+3i\sin\varphi-4i\sin^3\varphi.$
1.495. Find and plot on the complex plane all roots of the 2nd, 3rd, and 4th powers of unity.
Solution.
Let's express the number 1 in exponential form:
$1=1e^{0i}$. That is, $r=1, \varphi=0$.
Next, using de Moivre's formula, we calculate the square root of unity:
$$z_0=\sqrt[2]{1}e^{i\left(\frac{0}{2}+\frac{2\pi}{2}0\right)}=e^0=1.$$$$z_1=\sqrt[2]{1}e^{i\left(\frac{0}{2}+\frac{2\pi}{2}1\right)}=e^{i\pi}=\cos\pi+i\sin\pi=-1.$$
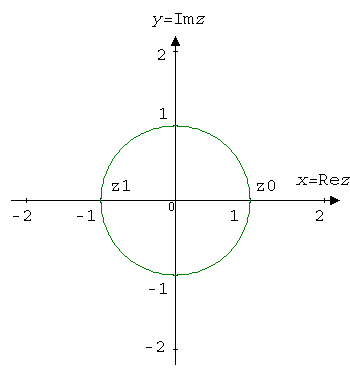
We calculate the cube root of unity:
$$z_0=\sqrt[3]{1}e^{i\left(\frac{0}{3}+\frac{2\pi}{3}0\right)}=e^0=1.$$
$$z_1=\sqrt[3]{1}e^{i\left(\frac{0}{3}+\frac{2\pi}{3}1\right)}=e^{i\frac{2\pi}{3}}=\cos\frac{2\pi}{3}+i\sin\frac{2\pi}{3}=-\frac{1}{2}+i\frac{\sqrt 3}{2}.$$
$$z_2=\sqrt[3]{1}e^{i\left(\frac{0}{3}+\frac{2\pi}{3}2\right)}=e^{i\frac{4\pi}{3}}=\cos\frac{4\pi}{3}+i\sin\frac{4\pi}{3}=-\frac{1}{2}-i\frac{\sqrt 3}{2}.$$
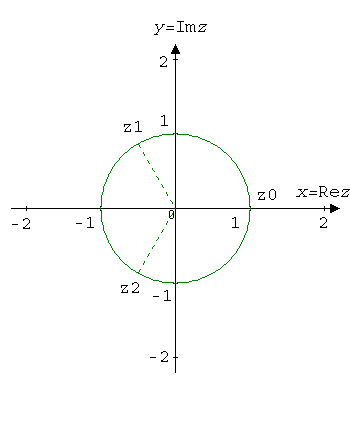
We calculate the fourth root of unity:
$$z_0=\sqrt[4]{1}e^{i\left(\frac{0}{4}+\frac{2\pi}{4}0\right)}=e^0=1.$$
$$z_1=\sqrt[4]{1}e^{i\left(\frac{0}{4}+\frac{2\pi}{4}1\right)}=e^{i\frac{\pi}{2}}=\cos\frac{\pi}{2}+i\sin\frac{\pi}{2}=i.$$
$$z_2=\sqrt[4]{1}e^{i\left(\frac{0}{4}+\frac{2\pi}{4}2\right)}=e^{i\pi}=\cos\pi+i\sin\pi=-1.$$
$$z_3=\sqrt[4]{1}e^{i\left(\frac{0}{4}+\frac{2\pi}{4}3\right)}=e^{i\frac{3\pi}{2}}=\cos\frac{3\pi}{2}+i\sin\frac{3\pi}{2}=-i.$$
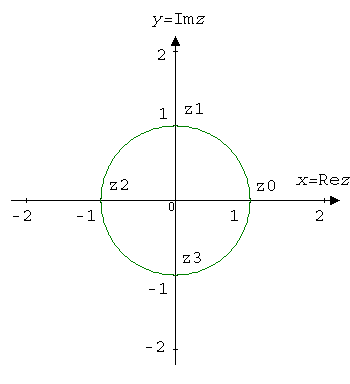
Answer: Roots of the second power: $z_0=1;,, z_1 =-1.$ Roots of the third power: $z_0=1;,, z_1=-\frac{1}{2}+i\frac{\sqrt{3}}{2};,, z_2=-\frac{1}{2}-i\frac{\sqrt{3}}{2}.$ Roots of the fourth power: $z_0=1;,, z_1=i;,, z_2=-1;,, z_3=-i.$
Find all values of the roots:
1.499. $\sqrt{-1+i\sqrt{3}}$.
Solution.
Let's express the number $z=-1+i\sqrt{3}$ in exponential form:
$r=\sqrt{x^2+y^2}=\sqrt{1+3}= 2$.
Since the number $z$ lies in the second quadrant, we have:
$\tan\varphi=\frac{y}{x}=\frac{\sqrt{3}}{-1}=-\sqrt{3}$ and $\varphi=\frac{2\pi}{3}$.
Thus, we can express the number $z=-1+i\sqrt{3}$ in exponential form: $z=2 e^{i\frac{2\pi}{3}}$.
Using de Moivre's formula, we calculate the square root of unity:
$$z_0=\sqrt{2}e^{i\left(\frac{2\pi}{6}+\frac{2\pi}{2}0\right)}=\sqrt 2e^{i\frac{\pi}{3}}=\sqrt 2\left(cos\frac{\pi}{3}+i\sin\frac{\pi}{3}\right)=\sqrt 2\left(\frac{1}{2}+i\frac{\sqrt 3}{2}\right).$$
$$z_1=\sqrt{2}e^{i\left(\frac{2\pi}{6}+\frac{2\pi}{2}1\right)}=\sqrt 2e^{i\frac{\pi}{3}+\pi}=\sqrt 2\left(cos\frac{4\pi}{3}+i\sin\frac{4\pi}{3}\right)=$$ $$=\sqrt 2\left(-\frac{1}{2}-i\frac{\sqrt 3}{2}\right).$$
Answer: $\pm\frac{\sqrt 2}{2}(1+i\sqrt 3)$
1.501. $\sqrt [5]{-1-i}.$
Solution.
Let's express the number $z=-1-i\sqrt{3}$ in exponential form:
$r=\sqrt{x^2+y^2}=\sqrt{1+3}= 2$.
Since the number $z$ lies in the third quadrant, we have:
$\tan\varphi=\frac{y}{x}=\frac{-\sqrt{3}}{-1}=\sqrt{3}$ and $\varphi=\frac{5\pi}{3}$.
Thus, we can express the number $z=-1-i\sqrt{3}$ in exponential form: $z=2 e^{i\frac{5\pi}{3}}$.
Using de Moivre's formula, we calculate the square root of unity:
$$z_0=\sqrt[5]{\sqrt 2}e^{i\left(\frac{5\pi}{4\cdot 5}+\frac{2\pi}{5}0\right)}=\sqrt [10] {2}e^{i\frac{\pi}{4}}=\sqrt[10]{2}\left(\cos\frac{\pi}{4}+i\sin\frac{\pi}{4}\right)=\sqrt[10]{2} \left(\frac{1}{\sqrt 2}+i\frac{1}{\sqrt 2}\right).$$
$$z_1=\sqrt[5]{\sqrt 2}e^{i\left(\frac{5\pi}{4\cdot 5}+\frac{2\pi}{5}1\right)}=\sqrt [10] {2}e^{i\frac{\pi}{4}}=\sqrt[10]{2}\left(\cos\frac{13\pi}{20}+i\sin\frac{13\pi}{20}\right).$$
$$z_2=\sqrt[5]{\sqrt 2}e^{i\left(\frac{5\pi}{4\cdot 5}+\frac{2\pi}{5}2\right)}=\sqrt [10] {2}e^{i\frac{21\pi}{20}}=\sqrt[10]{2}\left(\cos\frac{21\pi}{20}+i\sin\frac{21\pi}{20}\right).$$
$$z_3=\sqrt[5]{\sqrt 2}e^{i\left(\frac{5\pi}{4\cdot 5}+\frac{2\pi}{5}3\right)}=\sqrt [10] {2}e^{i\frac{29\pi}{20}}=\sqrt[10]{2}\left(\cos\frac{29\pi}{20}+i\sin\frac{29\pi}{20}\right).$$
$$z_4=\sqrt[5]{\sqrt 2}e^{i\left(\frac{5\pi}{4\cdot 5}+\frac{2\pi}{5}4\right)}=\sqrt [10] {2}e^{i\frac{37\pi}{20}}=\sqrt[10]{2}\left(\cos\frac{37\pi}{20}+i\sin\frac{37\pi}{20}\right).$$
Answer: $\sqrt[10]{2}\left(\cos\left(\frac{\pi}{4}+\frac{2\pi}{5}k\right)+i\sin\left(\frac{\pi}{4}+\frac{2\pi}{5}k\right)\right).$
Homework:
1.483. Prove Euler's formula $\sin\varphi=\frac{e^{i\varphi}-e^{-i\varphi}}{2i}$.
Using de Moivre's formula, calculate the following expressions:
1.486. $\frac{(1+i)^{5}}{(1-i)^3}$.
Answer: $2.$
1.488. $(1+i)^8(1-i\sqrt 3)^{-6}$.
Answer: $\frac{1}{4}.$
Using de Moivre's formula, express the following functions in terms of $\cos\varphi$ and $\sin\varphi$:
1.492. $\sin 3\varphi$.
Answer: $3\sin\varphi-4\sin^3\varphi.$
1.493. $\cos 4\varphi$.
Answer: $\cos^4\varphi-6\cos^2\varphi\sin^2\varphi+\sin^4\varphi.$
Find all values of the roots:
1.496. $\sqrt i$
Answer: $\pm\frac{\sqrt 2}{2}\left(1+i\right).$
1.497. $\sqrt {-1}$.
Answer: $\pm\frac{\sqrt 2}{2}\left(1+i\right),$ $\pm\frac{\sqrt 2}{2}\left(1-i\right).$
1.500. $\sqrt[4]{2\sqrt 3+2i}$.
Answer: $\sqrt{2}\left(\cos\left(\frac{\pi}{24}+\frac{\pi}{2}k\right)+i\sin\left(\frac{\pi}{24}+\frac{\pi}{2}k\right)\right).$
1.502. $\sqrt[6]{1+i\sqrt 3}$.
Answer: $\sqrt[6]{2}\left(\cos\left(\frac{\pi}{18}+\frac{\pi}{3}k\right)+i\sin\left(\frac{\pi}{18}+\frac{\pi}{3}k\right)\right).$


