The distance between two intersecting lines.

Let $L_1: \frac{x-x_1}{m_1}=\frac{y-y_1}{l_1}=\frac{z-z_1}{k_1}$ and $L_2: \frac{x-x_2}{m_2}=\frac{y-y_2}{l_2}=\frac{z-z_2}{k_2}$ be two intersecting lines. The distance $\rho(L_1, L_2)$ between the lines $L_1$ and $L_2$ can be found using the following procedure:

1) Find the equation of the plane $P$ passing through the line $L_1$ and parallel to the line $L_2$:

The plane $P$ passes through the point $M_1(x_1, y_1, z_1)$, perpendicular to the vector $\overline{n}=[\overline{s_1}, \overline{s_2}]=(n_x, n_y, n_z)$, where $\overline{s_1}=(m_1, l_1, k_1)$ and $\overline{s_2}=(m_2, l_2, k_2)$ are the direction vectors of the lines $L_1$ and $L_2$ respectively. Therefore, the equation of the plane $P$ is $n_x(x-x_1)+n_y(y-y_1)+n_z(z-z_1)=0$.

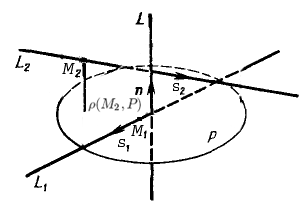
2) The distance between the lines $L_1$ and $L_2$ is equal to the distance from any point on the line $L_2$ to the plane $P$.

$$\rho(L_1, L_2)=\rho (M_2, P)=\left|\frac{n_x x_2+n_y y_2+n_z z_2}{\sqrt{n_x^2+n_y^2+n_z^2}}\right|.$$

Finding the common perpendicular of intersecting lines.

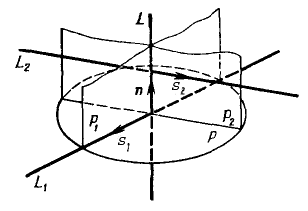
To find the common perpendicular of the intersecting lines $L_1$ and $L_2$, it is necessary to find the equations of the planes $P_1$ and $P_2$ passing through the lines $L_1$ and $L_2$ respectively, perpendicular to the plane $P$.

Let $P_1: A_1x+B_1y+C_1z+D_1=0;$

$P_2: A_2x+B_2y+C_2z+D_2=0.$

Then the equation of the common perpendicular has the form

$\left\{\begin{array}{lcl}A_1x+B_1y+C_1z+D_1=0;\\ A_2x+B_2y+C_2z+D_2=0.\end{array}\right. $

Example.

2.214.

For the given lines $L_1: \frac{x+7}{3}=\frac{y+4}{4}=\frac{z+3}{-2}$ and $L_2:\frac{x-21}{6}=\frac{y+5}{-4}=\frac{z-2}{-1}$, it is required to:

a) prove that the lines do not lie in the same plane, i.e., they are intersecting;

b) write the equation of the plane passing through the line $L_2$ parallel to $L_1$;

c) calculate the distance between the lines;

d) write the equations of the common perpendicular to the lines $L_1$ and $L_2$.

Solution.

a) If the lines $L_1$ and $L_2$ lie in the same plane, then their direction vectors $\overline{s_1}(3, 4, -2)$, $\overline{s_2}(6, -4, -1)$, and the vector $\overline l$, connecting an arbitrary point on line $L_1$ and an arbitrary point on line $L_2$, are coplanar. As such a vector $\overline{l}$, we can choose $\overline{l}(x_2-x_1, y_2-y_1, z_2-z_1)$. Let's check whether these vectors are coplanar.

$$\begin{vmatrix}21-(-7)&-5-(-4)&2-(-3)\\3&4&-2\\6&-4&-1\end{vmatrix}= \begin{vmatrix}28&-1&5\\3&4&-2\\6&-4&-1\end{vmatrix}=$$ $$=28\cdot 4\cdot(-1)+3\cdot(-4)\cdot 5+(-1)\cdot (-2)\cdot 6-$$ $$-6\cdot 4\cdot 5-(-4)\cdot(-2)\cdot 28-3\cdot(-1)\cdot (-1)=$$

$$-112-60+12-120-224+3=501\neq 0.$$

Therefore, the vectors are not coplanar, and the lines do not lie in the same plane.

b) Let's write down the equation of the plane passing through the line $L_2$ parallel to $L_1$. This plane passes through the point $M_2(21, -5, 2)$ perpendicular to the vector $\overline n=[\overline s_1, \overline s_2]$.

$$[s_1, s_2]=\begin{vmatrix}i&j&k\\3&4&-2\\6&-4&-1\end{vmatrix}=i\begin{vmatrix}4&-2\\-4&-1\end{vmatrix}-j\begin{vmatrix}3&-2\\6&-1\end{vmatrix}+k\begin{vmatrix}3&4\\6&-4\end{vmatrix}=$$ $$=i(-4-8)-j(-3+12)+k(-12-24)=-12i-9j-36k.$$

Thus, the vector $\overline n$ has coordinates $\overline n(-12, -9, -36)$.

Let's find the equation of the plane: $$P:\,\, -12(x-21)-9(y+5)-36(z-2)=0\Rightarrow$$ $$\Rightarrow-12x-9y-36z+252-45+72=0\Rightarrow -12x-9y-36z+279=0\Rightarrow$$ $$\Rightarrow 4x+3y+12z-93=0.$$

Answer: $4x+3y+12z-93=0.$

c) The distance between the lines $L_1$ and $L_2$ is equal to the distance from any point on line $L_1$ to the plane $P$:

$$\rho(L_1, L_2)=\rho(M_1, P)=\left|\frac{n_xx_1+n_yy_1+n_zz_1}{\sqrt{n_x^2+n_y^2+n_z^2}}\right|$$ $$\rho(M_1, P)= \left|\frac{4(-7)+3(-4)+12(-3)}{\sqrt{4^2+ 3^2+12^2}}\right|= \left|\frac{-28-12-36}{\sqrt{16+9+144}}\right|=$$ $$=\left|\frac{-76}{\sqrt{169}}\right|=\frac{76}{13}.$$

Answer: $\frac{76}{13}$.

g) Let's find the equations of planes $P_1$ and $P_2$ passing through lines $L_1$ and $L_2$, respectively, perpendicular to the plane $P$.

We have $M_1=(-7, -4, -3)\in P_1$,

$$\overline n_1=[\overline{s}_1, \overline{n}] =\begin{vmatrix}i&j&k\\3&4&-2\\4&3&12\end{vmatrix}=i\begin{vmatrix}4&-2\\3&12\end{vmatrix}-j\begin{vmatrix}3&-2\\4&12\end{vmatrix}+k\begin{vmatrix}3&4\\4&3\end{vmatrix}=$$ $$=i(48+6)-j(36+8)+k(9-16)=54i-44j-7k.$$

Thus,$$P_1: 54(x+7)-44(y+4)-7(z+3)=54x-44y-7z+378-176-21=$$ $$=54x-44y-7z+181=0.$$

Similarly, we find $P_2$:

We have $M_2=(21, -5, 2)\in P_2$,

$$\overline n_2=[\overline{s}_2, \overline{n}] =\begin{vmatrix}i&j&k\\6&-4&-1\\4&3&12\end{vmatrix}=i\begin{vmatrix}-4&-1\\3&12\end{vmatrix}-j\begin{vmatrix}6&-1\\4&12\end{vmatrix}+k\begin{vmatrix}6&-4\\4&3\end{vmatrix}=$$ $$=i(-48+3)-j(72+4)+k(18+16)=-45i-76j+34k.$$

Thus, $$P_1: -45(x-21)-76(y+5)+34(z-2)=-45x-76y+34z+945-380-68=$$ $$=-45x-76y+34z+497=0.$$

Answer: $\left\{\begin{array}{lcl}54x-44y-7z+181=0;\\ -45x-76y+34z+497=0.\end{array}\right. $

Homework.

2.215.

For the given lines $L_1: \frac{x-6}{3}=\frac{y-3}{-2}=\frac{z+3}{4}$ and $L_2:\frac{x+1}{3}=\frac{y+7}{-3}=\frac{z-4}{8}$, it is required to:

a) prove that the lines do not lie in the same plane, i.e., they intersect;

b) write the equation of the plane passing through the line $L_2$ parallel to $L_1$;

c) calculate the distance between the lines;

d) write the equations of the common perpendicular to the lines $L_1$ and $L_2$.

Answer:

b) $4x+12y+12z+76=0$;

c) $\frac{127}{13}$;

d) $\left\{\begin{array}{lcl}53x-7y-44z-429=0;\\ 105x-23y-48z+136=0.\end{array}\right. $