Line on a Plane, Various Equations.
There are such forms of writing the equation of a line:
1) $y = kx + b,$ where $k$ is the slope coefficient, and $b$ is the segment the line cuts off on the $OY$ axis.
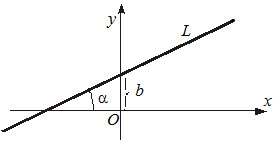
2) $y - y_0 = k(x - x_0)$ - the equation of the line passing through a given point $P(x_0, y_0)$ at a given angle $\alpha$ to the $OX$ axis ($k = \tan\alpha$).
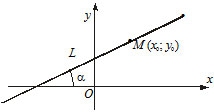
3) $\frac{x - x_1}{x_2 - x_1} = \frac{y - y_1}{y_2 - y_1}$ - the equation of the line passing through two points $M(x_1, y_1)$ and $N(x_2, y_2)$.
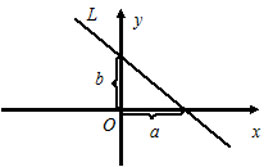
4) $\frac{x}{a} + \frac{y}{b} = 1$ - the line equation in intercept form on the axes, where $a$ and $b$ are the lengths of the segments that the line cuts off on the coordinate axes.

5) $\frac{x - x_0}{l} = \frac{y - y_0}{m}$ - the canonical equation of the line, where $\overline{S} = (l, m)$ is the direction vector of the line, i.e., a vector parallel to the line ($\overline{S} \parallel L$), with point $P(x_0, y_0) \in L$.
6) $A(x - x_0) + B(y - y_0) = 0$ - the equation of the line $L$, passing through the point $M(x_0, y_0)$ perpendicular to the vector $\overline{N} = (A, B)$. The vector $\overline{N}$ is called the normal vector of the line.
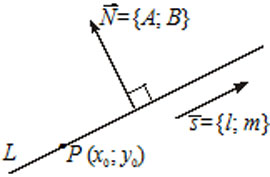
$Ax + By + C = 0$ - the general equation of the line $L$, where $\overline{N} = (A, B)$ is the normal vector of the line $L$.
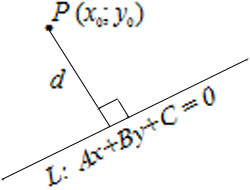
$x \cos \alpha + y \cos \beta - p = 0$ - the normal form of the line equation, where $\cos \alpha$ and $\cos \beta$ are the directional cosines of the normal vector $n$, directed from the origin towards the line, and $p > 0$ is the distance from the origin to the line.
The general equation of the line is converted to the normal form by multiplying by the normalizing factor $\mu = -\frac{\text{sgn } C}{\sqrt{A^2 + B^2}}.$
The distance from the point $P(x_0, y_0)$ to the line $L: Ax + By + C = 0$ is calculated using the formula$$d=\left|\frac{Ax_0+By_0+C}{\sqrt{A^2+B^2}}\right|.$$
The positioning of two lines on the plane.
Conditions for the parallelism of two lines:
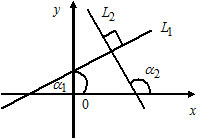
1) Let $L_1: k_1x + b_1,$ $k_1 = \tan \alpha_1;$
$L_2: k_2x + b_2,$ $k_2 = \tan \alpha_2.$
Lines $L_1$ and $L_2$ are parallel if and only if $k_1 = k_2.$
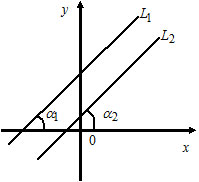
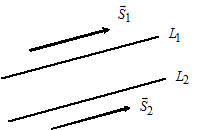
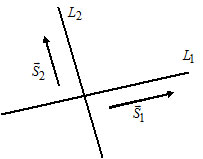
2) Let $L_1: \frac{x - x_1}{l_1} = \frac{y - y_1}{m_1},$ $\overline{S}_1 = (l_1, m_1);$
$L_2: \frac{x - x_2}{l_2} = \frac{y - y_2}{m_2},$ $\overline{S}_2 = (l_2, m_2).$
Lines $L_1$ and $L_2$ are parallel if and only if $\overline{S}_1 \parallel \overline{S}_2 \Leftrightarrow \frac{l_1}{l_2} = \frac{m_1}{m_2}.$
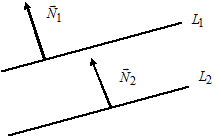
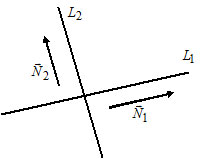
3)Let $L_1: A_1x + B_1y + C_1 = 0,$ $\overline{N}_1 = (A_1, B_1);$
$L_2: A_2x + B_2y + C_2 = 0,$ $\overline{N}_2 = (A_2, B_2).$
Lines $L_1$ and $L_2$ are parallel if and only if $\overline{N}_1 \parallel \overline{N}_2 \Leftrightarrow \frac{A_1}{A_2} = \frac{B_1}{B_2}.$
Conditions for the perpendicularity of two lines:
1) Let $L_1: k_1x + b_1,$ $k_1 = \tan \alpha_1;$
$L_2: k_2x + b_2,$ $k_2 = \tan \alpha_2.$
$L_1 \perp L_2 \Leftrightarrow k_1 \cdot k_2 = -1.$
2) Let $L_1: \frac{x - x_1}{l_1} = \frac{y - y_1}{m_1},$ $\overline{S}_1 = (l_1, m_1);$
$L_2: \frac{x - x_2}{l_2} = \frac{y - y_2}{m_2},$ $\overline{S}_2 = (l_2, m_2).$
$L_1 \perp L_2 \Leftrightarrow \overline{S}_1 \perp \overline{S}_2 \Leftrightarrow l_1 \cdot l_2 + m_1 \cdot m_2 = 0.$
3) Let $L_1: A_1x + B_1y + C_1 = 0,$ $\overline{N}_1 = (A_1, B_1);$
$L_2: A_2x + B_2y + C_2 = 0,$ $\overline{N}_2 = (A_2, B_2).$
$L_1 \perp L_2 \Leftrightarrow \overline{N}_1 \perp \overline{N}_2 \Leftrightarrow A_1 \cdot A_2 + B_1 \cdot B_2 = 0.$
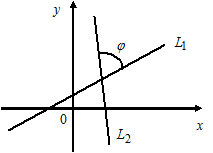
The angle between two lines:
1) Let $L_1: k_1x + b_1,$ $k_1 = \tan \alpha_1;$
$L_2: k_2x + b_2,$ $k_2 = \tan \alpha_2.$
$\tan(\widehat{(L_1, L_2)}) = \frac{k_1 - k_2}{1 + k_1 \cdot k_2}.$
2) Let $L_1: \frac{x - x_1}{l_1} = \frac{y - y_1}{m_1},$ $\overline{S}_1 = (l_1, m_1);$
$L_2: \frac{x - x_2}{l_2} = \frac{y - y_2}{m_2},$ $\overline{S}_2 = (l_2, m_2).$
$\cos(\widehat{(L_1, L_2)}) = \frac{l_1 \cdot l_2 + m_1 \cdot m_2}{\sqrt{l_1^2 + m_1^2} \cdot \sqrt{l_2^2 + m_2^2}}.$
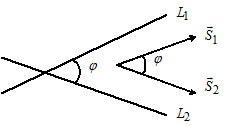
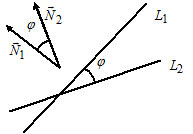
3) Let $L_1: A_1x + B_1y + C_1 = 0,$ $\overline{N}_1 = (A_1, B_1);$
$L_2: A_2x + B_2y + C_2 = 0,$ $\overline{N}_2 = (A_2, B_2).$
$\cos(\widehat{(L_1, L_2)}) = \frac{A_1 \cdot A_2 + B_1 \cdot B_2}{\sqrt{A_1^2 + B_1^2} \cdot \sqrt{A_2^2 + B_2^2}}.$
Examples:
2.141.
Solution:
a) The line $L$ is defined by the point $M_0(-1; 2) \in L$ and the normal vector $\overline{N}(2; 2)$. Required: 1) Write the equation of the line, bring it to general form, and construct the line; 2) Convert the general equation to the normal form and indicate the distance from the origin to the line.
By substituting into formula 6) for the line equation ($A(x - x_0) + B(y - y_0) = 0$) the coordinates of the point $(x_0; y_0) = M_0(-1; 2)$ and the vector $(A; B) = \overline{N}(2; 2)$, we get:
$2(x + 1) + 2(y - 2) = 0.$ Now, let's bring this equation to the general form:
$2x + 2 + 2y - 4 = 0 \Rightarrow$
$2x + 2y - 2 = 0 \Rightarrow$
$x + y - 1 = 0.$
The normal form of the line equation looks like $x \cos \alpha + y \cos \beta - p = 0$, where $\cos \alpha$ and $\cos \beta$ are the directional cosines of the normal vector $n$, directed from the origin towards the line, and $p > 0$ is the distance from the origin to the line.
The general equation of the line is converted to the normal form by multiplying by the normalizing factor $\mu = -\frac{\text{sgn } C}{\sqrt{A^2 + B^2}}.$
For our line, we have $A = 1; B = 1; C = -1 \Rightarrow \text{sgn } C = -1.$ Thus, $\mu = -\frac{-1}{\sqrt{1 + 1}} = \frac{1}{\sqrt{2}}.$
Write the normal equation of the line:
$x + y - 1 = 0 \cdot \frac{1}{\sqrt{2}} \Rightarrow$
$\frac{1}{\sqrt{2}}x + \frac{1}{\sqrt{2}}y - \frac{1}{\sqrt{2}} = 0.$
The distance from the origin is $p = \frac{1}{\sqrt{2}}.$
Answer: $2(x + 1) + 2(y - 2) = 0;$ general equation $x + y - 1 = 0;$ normal equation of the line $\frac{1}{\sqrt{2}}x + \frac{1}{\sqrt{2}}y - \frac{1}{\sqrt{2}} = 0;$ $p = \frac{1}{\sqrt{2}}.$
{loadposition user1}
2.142
a) The line $L$ is defined by the point $M_0(-1; 2) \in L$ and the direction vector $\overline{S}(3; -1)$. Required: 1) Write the equation of the line, bring it to the general form, and construct the line; 2) Convert the general equation to the normal form and indicate the distance from the origin to the line.
Solution:
Substitute into formula 5) for line equations ($\frac{x - x_0}{l} = \frac{y - y_0}{m}$) the coordinates of the point $(x_0; y_0) = M_0(-1; 2)$ and the vector $(l; m) = \overline{S}(3; -1):$ $\frac{x + 1}{3} = \frac{y - 2}{-1}$
Now, let's bring this equation to the general form:
$-1(x + 1) = 3(y - 2) \Rightarrow$
$-x - 1 - 3y + 6 = 0 \Rightarrow$
$x + 3y - 5 = 0.$
The general equation of the line is converted to the normal form by multiplying by the normalizing factor $\mu = -\frac{\text{sgn } C}{\sqrt{A^2 + B^2}}.$
For our line, we have $A = 1; B = 3; C = -5 \Rightarrow \text{sgn } C = -1.$ Thus, $\mu = -\frac{-1}{\sqrt{1 + 9}} = \frac{1}{\sqrt{10}}.$
Write the normal equation of the line:
$x + 3y - 5 = 0 |\cdot \frac{1}{\sqrt{10}} \Rightarrow$
$\frac{1}{\sqrt{10}}x + \frac{3}{\sqrt{10}}y - \frac{5}{\sqrt{10}} = 0.$
The distance from the origin is $p = \frac{5}{\sqrt{10}}.$
Answer: $\frac{x + 1}{3} = \frac{y - 2}{-1};$ general equation $x + 3y - 5 = 0;$ normal equation of the line $\frac{1}{\sqrt{10}}x + \frac{3}{\sqrt{10}}y - \frac{5}{\sqrt{10}} = 0;$ $p = \frac{5}{\sqrt{10}}.$
2.143.
a) The line $L$ is given by its two points $M_1(1; 2) \in L$ and $M_2(-1; 0) \in L$. Required: 1) Write the equation of the line, bring it to the general form and construct the line; 2) Convert the general equation to the normal form and indicate the distance from the origin to the line.
Solution.
Substitute into formula 3) for the line equations ($\frac{x - x_1}{x_2 - x_1} = \frac{y - y_1}{y_2 - y_1}$) the coordinates of the points $M_1(1; 2) = (x_1; y_1)$ and $M_2(-1; 0) = (x_2; y_2):$ $\frac{x - 1}{-1 - 1} = \frac{y - 2}{0 - 2} \Rightarrow \frac{x - 1}{-2} = \frac{y - 2}{-2}.$
Next, let's bring this equation to the general form:
$-2(x - 1) = -2(y - 2) \Rightarrow$
$x - 1 = y - 2 \Rightarrow$
$x - y + 1 = 0.$
The general equation of the line is converted to the normal form by multiplying by the normalizing factor $\mu = -\frac{\text{sgn } C}{\sqrt{A^2 + B^2}}.$
For our line, we have $A = 1; B = -1; C = 1 \Rightarrow \text{sgn } C = 1.$ Thus, $\mu = -\frac{1}{\sqrt{1 + 1}} = -\frac{1}{\sqrt{2}}.$
Write the normal equation of the line:
$x - y + 1 = 0 |\cdot -\frac{1}{\sqrt{2}} \Rightarrow$
$-\frac{1}{\sqrt{2}}x + \frac{1}{\sqrt{2}}y - \frac{1}{\sqrt{2}} = 0.$
The distance from the origin is $p = \frac{1}{\sqrt{2}}.$
Answer: $\frac{x - 1}{-2} = \frac{y - 2}{-2};$ general equation $x - y + 1 = 0;$ normal equation of the line $-\frac{1}{\sqrt{2}}x + \frac{1}{\sqrt{2}}y - \frac{1}{\sqrt{2}} = 0;$ $p = \frac{1}{\sqrt{2}}.$
2.150.
For triangle $ABC$ given by the vertices $A(1; 2), B(2; -2), C(6; 1)$:
Find the equation of side $AB;$
Find the equation of altitude $CD$ and calculate its length $h = |CD|;$
Find the angle between the altitude $CD$ and the median $BM.$
Solution:
Let's create a diagram:
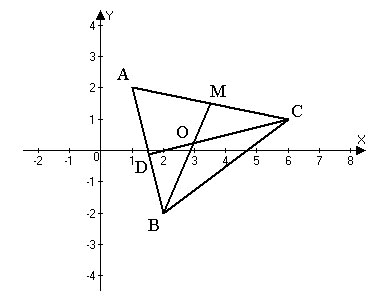
The equation of the line $AB$ can be found using the formula for a line passing through two points $\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}. $
In our case, we have $(x_1; y_1) = A(1; 2)$ and $(x_2; y_2) = B(2; -2)$.
We substitute the points' coordinates into the line equation. We obtain $$\frac{x-1}{2-1}=\frac{y-2}{-2-2}\Rightarrow x-1=\frac{y-2}{-4}.$$ Now, let's write down the general equation of the line $AB$:
$-4(x - 1) = y - 2 \Rightarrow -4x + 4 = y - 2 \Rightarrow 4x + y - 6 = 0.$
2) The equation of line $CD$ can be found using equation (6): $A(x - x_0) + B(y - y_0) = 0$ - the equation of the line $L$ that passes through point $M(x_0, y_0)$ perpendicular to vector $\overline{N} = (A, B)$.
In our case, the altitude $CD$ is the line that passes through point $C$ perpendicular to the vector $AB$.
Thus, we have, $$(x_0; y_0)=C=(6; 1);\quad\overline{N}=\overline{AB}=(2-1; -2-2)=(1; -4).$$
We substitute these coordinates into the line equation:
$1(x-6)-4(y-1)=0\Rightarrow x-6-4y+4=0 \Rightarrow x-4y-2=0.$
Therefore, the equation of the line $CD:$ $x-4y-2=0.$
To find the length of altitude $h = |CD|$, we need to find the coordinates of point $D$, the intersection of lines $CD$ and $AB$:
$\left\{\begin{array}{lcl}x-4y-2=0\\4x+y-6=0.\end{array}\right. $
Solve the system of equations using the method of elimination:
$\left\{\begin{array}{lcl}x-4y-2=0\\4x+y-6=0.\end{array}\right. \Rightarrow$ $\left\{\begin{array}{lcl}x=4y+2\\4x+y-6=0.\end{array}\right. \Rightarrow$
$\left\{\begin{array}{lcl}x=4y+2\\4(4y+2)+y-6=0.\end{array}\right. \Rightarrow$ $\left\{\begin{array}{lcl}x=4y+2\\16y+8+y-6=0.\end{array}\right. \Rightarrow$
$\left\{\begin{array}{lcl}x=-8/17+2=26/17\\y=-2/17.\end{array}\right. .$
Therefore, we have $D\left(\frac{26}{17}, -\frac{2}{17}\right)$. Now we can find the length of the altitude $CD$:
$h=|CD|=\sqrt{(x_d-x_c)^2+(y_d-y_c)^2}=\sqrt{(26/17-6)^2+(-2/17-1)^2}=$ $\sqrt{\left(\frac{26-102}{17}\right)^2+\left(\frac{-2-17}{17}\right)^2}=\sqrt{\frac{76^2+19^2}{17^2}}=\sqrt{\frac{6137}{17^2}}=\frac{19}{17}\sqrt{17}=\frac{19}{\sqrt{17}}.$
3) The equation of the altitude $CD$ has already been found in step 2). Let's find the equation of the median $BM$. We will find it using the formula for the equation of a line passing through two points.
The coordinates of point $B=(2, -2);$ the coordinates of point $M$ can be found as the midpoint of side $AC:$ $x_M=\frac{x_A+x_C}{2}; y_M=\frac{y_A+y_C}{2}.$
$x_M=\frac{1+6}{2}=3.5;$ $y_M=\frac{2+1}{2}=1.5.$
Substitute the coordinates of points $B(2; -2)$ and $M(3.5; 1.5)$ into the equation of the line.
$\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}:$
$\frac{x-2}{3.5-2}=\frac{y-(-2)}{1.5-(-2)}\Rightarrow \frac{x-2}{1.5}=\frac{y+2}{3.5}\Rightarrow$
$3.5(x-2)=1.5(y+2)\Rightarrow 3.5x-7=1.5y+3 \Rightarrow 3.5x-1.5y-10=0.$
Next, knowing the general equations of the two lines $CD: x-4y-2=0$ and $BM: 3.5x-1.5y-10=0$, we can find the angle between them using the formula
$\cos\widehat{(L_1, L_2)}=$ $\frac{{A_1}\cdot{A_2}+{B_1}\cdot{B_2}}{\sqrt{A_1^2+B_1^2}\cdot\sqrt{A_2^2+B_2^2}},$
where $L_1: A_1x+B_1y+C_1=0,$ $\overline{N}_1=(A_1, B_1);$
$L_2: A_2x+B_2y+C_2=0,$ $\overline{N}_2=(A_2, B_2).$
For our lines, we have: $(A_1, B_1) = (1, -4)$ and $(A_2, B_2) = (3.5, -1.5)$.
From here,
$\cos\widehat{(CD, BM)}=$ $\frac{{1}\cdot{3.5}+{(-4)}\cdot{(-1.5)}}{\sqrt{1^2+(-4)^2}\cdot\sqrt{3.5^2+(-1.5)^2}}=\frac{9.5}{\sqrt{17}\cdot\sqrt{14.5}}=\frac{19}{\sqrt{986}}.$
Answer: 1) $AB: 4x+y-6=0.$
2) $CD:$ $x-4y-2=0; $ $h=|CD|=\frac{19}{\sqrt{17}};$
3) $\cos\widehat{(CD, BM)}=$ $\frac{19}{\sqrt{986}}.$
2.160. In the isosceles triangle $ABC$, the vertex $C$ is given as $(4, 3)$, the equation of the base $AC$ is $2x-y-5=0$, and the equation of the side $AB$ is $x-y=0$. Find the equation of the side $BC$.
Solution.
Let's find the coordinates of the vertex $A$ as the intersection point of the lines $AB$ and $AC$:
$$\left\{\begin{array}{lcl}x-y=0\\2x-y-5=0\end{array}\right.\Rightarrow\left\{\begin{array}{lcl}x=y\\2y-y-5=0\end{array}\right.\Rightarrow\left\{\begin{array}{lcl}x=y\\y=5\end{array}\right.\Rightarrow\left\{\begin{array}{lcl}x=5\\y=5\end{array}\right. $$
Thus, we have the coordinates of the vertices at the base of the isosceles triangle as $A(5, 5)$ and $C(4, 3)$. Let's find the coordinates of the vertex $B(x, y)$. We know that this point belongs to the line $AB: x-y=0$ and that $AB=BC$. Let's write down the formulas for the lengths of the sides $AB$ and $BC$:
$|AB|=\sqrt{(x-5)^2+(y-5)^2};$
$|BC|=\sqrt{(x-4)^2+(y-3)^2}.$
Next, to find the coordinates of point $B$, let's solve the system of equations:
$$\left\{\begin{array}{lcl}x-y=0\\\sqrt{(x-5)^2+(y-5)^2}=\sqrt{(x-4)^2+(y-3)^2}\end{array}\right.\Rightarrow$$ $$\left\{\begin{array}{lcl}x-y=0\\x^2-10x+25+y^2-10y+25=x^2-8x+16+y^2-6y+9\end{array}\right.\Rightarrow $$
$$\left\{\begin{array}{lcl}x-y=0\\-2x-4y+25=0\end{array}\right.\Rightarrow\left\{\begin{array}{lcl}x=y\\-2y-4y+25=0\end{array}\right.\Rightarrow $$
$$\Rightarrow\left\{\begin{array}{lcl}x=y\\y=\frac{25}{6}.\end{array}\right.$$ We found the coordinates of point$B\left(\frac{25}{6}, \frac{25}{6}\right).$
Knowing the coordinates of points $B$ and $C$, we can write the equation of line $BC$ as a line passing through two points $\left(\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1} \right):$
$$\frac{x-4}{\frac{25}{6}-4}=\frac{y-3}{\frac{25}{6}-3}\Rightarrow \frac{x-4}{\frac{25-24}{6}}=\frac{y-3}{\frac{25-18}{6}}\Rightarrow $$
$$\Rightarrow\frac{x-4}{1}=\frac{y-3}{7}\Rightarrow 7x-28=y-3\Rightarrow 7x-y-25=0.$$
Answer: $7x-y-25=0.$
2.165. Given two opposite vertices of a square $A(1; 3)$ and $C(-1; 1)$. Find the coordinates of the other two vertices and write down the equations of its sides.
Solution:
Let's find the equation of the diagonal $AC$:
$\frac{x-1}{-1-1}=\frac{y-3}{1-3} \Rightarrow \frac{x-1}{-2}=\frac{y-3}{-2}\Rightarrow x-y+2=0.$
Let's find its midpoint: $$x_O=\frac{x_A+x_C}{2}; y_O=\frac{y_A+y_C}{2}.$$
$$x_O=\frac{1-1}{2}=0;\,\,\, y_O=\frac{3+1}{2}=2\,\, \Rightarrow\,\, O=(0; 2).$$
Next, let's find the equation of the second diagonal of the square - the line passing through point $O$ perpendicular to the line $AC.$ For the line $AC$, the normal vector has coordinates $\overline{N}=(1; -1).$ The line perpendicular to the line $AC$ is parallel to the normal vector $\overline{N}$. Therefore, the equation of the line $BD$ is written using formula 5) $\left(\frac{x-x_0}{l}=\frac{y-y_0}{m}\right),$ where $(x_0, y_0)=O(0; 2),$ $(l, m)=\overline{N}=(1, -1):$
$$\frac{x}{1}=\frac{y-2}{-1}\Rightarrow x=-y+2 \Rightarrow x+y-2=0.$$
It is clear that $AO=CO=BO=DO.$ Let's find the length of segment $AO:$ $AO=\sqrt{(0-1)^2+(2-3)^2}=\sqrt{2}.$
Next, we will look for the coordinates of points $B$ and $D$ that lie on the line $BD$ and satisfy $BO=DO=AO.$
$$\left\{\begin{array}{lcl}x+y-2=0\\\sqrt{(0-x)^2+(2-y)^2}=\sqrt{2}\end{array}\right.\Rightarrow$$
$$\left\{\begin{array}{lcl}x=2-y\\\sqrt{(y-2)^2+(2-y)^2}=\sqrt{2}\end{array}\right.\Rightarrow$$
$$\left\{\begin{array}{lcl}x=2-y\\|2-y|\sqrt{2}=\sqrt{2}\end{array}\right.\Rightarrow\left\{\begin{array}{lcl}x=2-y\\|2-y|=1\end{array}\right.\Rightarrow\left\{\begin{array}{lcl}x=2-y\\\left[\begin{array}{lcl}2-y_1=1\\2-y_2=-1\end{array}\right.\end{array}\right.\Rightarrow$$
$\Rightarrow\left\{\begin{array}{lcl}x=2-y\\\left[\begin{array}{lcl}y_1=1\\y_2=3\end{array}\right.\end{array}\right.\Rightarrow$ $\left\{\begin{array}{lcl}\left[\begin{array}{lcl}x_1=1\\x_2=-1\end{array}\right.\\\left[\begin{array}{lcl}y_1=1\\y_2=3\end{array}\right.\end{array}\right.$
Thus, we have found the coordinates of vertices $B(1; 1)$ and $D(-1; 3).$ Knowing the coordinates of the square's vertices, let's write the equations of its sides using formula (3) - $\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1} $ - the equation of a line passing through two points $M(x_1, y_1)$ and $N(x_2, y_2).$
$A(1; 3),$ $B(1; 1),$ $C(-1; 1),$ $D(-1; 3).$
$AB:$ $\frac{x-1}{1-1}=\frac{y-3}{1-3}\Rightarrow\frac{x-1}{0}=\frac{y-3}{-2}\Rightarrow $ $-2(x-1)=0\Rightarrow x=1.$
$BC:$ $\frac{x-1}{-1-1}=\frac{y-1}{1-1}\Rightarrow\frac{x-1}{-1}=\frac{y-1}{0}\Rightarrow $ $0(x-1)=-1(y-1)\Rightarrow y=1.$
$CD:$ $\frac{x+1}{-1+1}=\frac{y-1}{3-1}\Rightarrow\frac{x+1}{0}=\frac{y-1}{2}\Rightarrow $ $2(x+1)=0(y-1)\Rightarrow x=-1.$
$DA:$ $\frac{x-1}{-1-1}=\frac{y-3}{3-3}\Rightarrow\frac{x-1}{-2}=\frac{y-3}{0}\Rightarrow $ $0(x-1)=-2(y-3)\Rightarrow y=3.$
Answer:$A(1; 3),$ $B(1; 1),$ $C(-1; 1),$ $D(-1; 3);$ $AB:$ $x=1;$ $BC:$ $y=1;$ $CD:$ $x=-1;$ $DA:$ $y=3.$


