Ellipse, hyperbola, parabola. Director property of ellipse and hyperbola.
Ellipse.
An ellipse with the canonical equation $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1, a\geq b>0,$ has the shape shown in the figure.
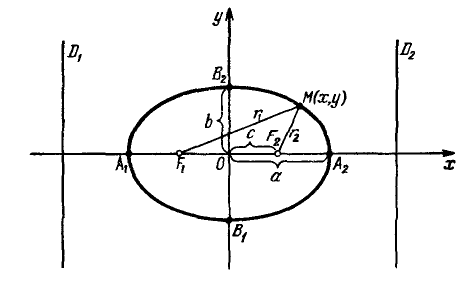
The parameters $a$ and $b$ are called the semi-axes of the ellipse (major and minor, respectively). The points $A_1(-a, 0),$ $A_2(a, 0), $ $B_1(0, -b),$ and $B_2(0, b),$ are its vertices. The axes of symmetry $Ox$ and $Oy$ are the principal axes, and the center of symmetry $O$ is the center of the ellipse.
The points $F_1(-c, 0)$ and $F_2(c, 0),$ where $c=\sqrt{a^2-b^2}\geq 0,$ are called the foci of the ellipse. The vectors $\overline{F_1M}$ and $\overline{F_2M}$ are the focal radius vectors, and the numbers $r_1=|\overline{F_1M}|$ and $r_2=|\overline{F_2M}|$ are the focal radii of the point $M$ belonging to the ellipse. In the special case where $a=b,$ the foci $F_1$ and $F_2$ coincide with the center, and the canonical equation takes the form $\frac{x^2}{a^2}+\frac{y^2}{a^2}=1,$ or $x^2+y^2=a^2,$ describing a circle with radius $a$ centered at the origin.
The number $e=\frac{c}{a}=\sqrt{1-\frac{b^2}{a^2}} ,, (0\leq e<1)$ is called the eccentricity of the ellipse and measures its "flatness" (when $e=0,$ the ellipse becomes a circle).
The lines $D_1: x=-a/e$ and $D_2: x=a/e,$ perpendicular to the major axis and passing at a distance $a/e$ from the center, are called the directrices of the ellipse.
Theorem. (Directorial property of an ellipse)
The ellipse is a set of points for which the ratio of the distances from each point to the focus and to the corresponding directrix is constant and equal to $e$.
Examples.
2.246. Construct the ellipse $9x^2+25y^2=225.$ Find: a) semi-axes; b) coordinates of the foci; c) eccentricity; d) equations of the directrices.
Solution.
Let's transform the equation of the ellipse into canonical form:
$$ 9x^2+25y^2=225 |:225\Rightarrow\frac{9x^2}{225}+\frac{25y^2}{225}=1\Rightarrow$$
$$\Rightarrow\frac{x^2}{25}+\frac{y^2}{9}=1\Rightarrow\frac{x^2}{5^2}+\frac{y^2}{3^2}=1.$$
a) Finding the semi-axes: $a=5,$ $b=3.$
b) The foci are found using the formulas $F_1(-c, 0)$ and $F_2(c, 0),$ where $c=\sqrt{a^2-b^2}:$
$c=\sqrt{5^2-3^2}=\sqrt{16}=4\Rightarrow F_1(-4, 0),\qquad F_2(4, 0).$
c) Eccentricity $e=\frac{c}{a}=\frac{4}{5}.$
d) Equations of the directrices are found using the formulas $D_1: x=-a/e$ and $D_2: x=a/e:$
$D_1: x=-\frac{5}{4/5}=-\frac{25}{4}$ and $D_2: x=\frac{5}{4/5}=\frac{25}{4}.$
Let's draw a diagram:
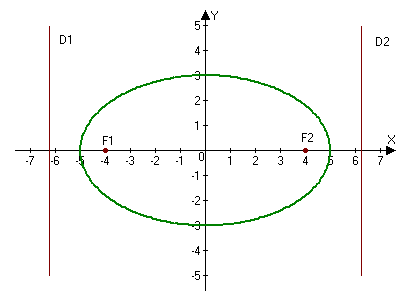
Answer: a) $a = 5,$ $b = 3;$ b) $F_1(-4, 0),$ $F_2(4, 0);$ c) $e = \frac{4}{5};$ d) $D_1: x = -\frac{25}{4}$ and $D_2: x = \frac{25}{4}.$
2.249 (a). Establish that the equation $5x^2 + 9y^2 - 30x + 18y + 9 = 0$ defines an ellipse, find its center $C,$ semi-axes, eccentricity, and equations of the directrices.
Solution.
To normalize the equation of the ellipse, we complete the squares:
$$5x^2+9y^2-30x+18y+9=(5x^2-30x)+(9y^2+18y)+9=$$
$$5(x^2+6x+9-9)+9(y^2+2y+1-1)+9=5(x+3)^2-45+9(y+1)^2-9+9=$$
$$5(x+3)^2+9(y+1)^2-45=0\Rightarrow5(x+3)^2+9(y+1)^2=45|:45\Rightarrow$$
$$ \frac{(x+3)^2}{9}+\frac{(y+1)^2}{5}=1\Rightarrow\frac{(x+3)^2}{3^2}+\frac{(y+1)^2}{(\sqrt 5)^2}=1.$$
This is the equation of an ellipse. The center has coordinates $C=(x_0, y_0)=(-3, -1);$ semi-axes $a=3,$ $b=\sqrt 5.$
$c=\sqrt{a^2-b^2}\Rightarrow c=\sqrt{9-5}=\sqrt 4=2\Rightarrow e=\frac{c}{a}=\frac{2}{3}.$
The equations of the directrices for an ellipse with the center at the origin are found using the formulas $D_1: x=-a/e$ and $D_2: x=a/e:$
$D_1: x=-\frac{3}{2/3}=-\frac{9}{2} $ and $D_2: x=\frac{3}{2/3}=\frac{9}{2}.$ Since the center of the given ellipse is shifted, the directrices will have equations $D_1: x=x_0-a/e$ and $D_2: x=x_0+a/e:$
$$D_1: x=3-\frac{9}{2}=\frac{6-9}{2}=-\frac{3}{2}\Rightarrow 2x+3=0 $$ $$D_2: x=3+\frac{9}{2}=\frac{6+9}{2}=\frac{15}{2}\Rightarrow2x-15=0.$$
Answer: $C=(x_0, y_0)=(-3, -1);$ $a=3,$ $b=\sqrt 5;$ $ e=\frac{2}{3}.$ $D_1:2x+3=0, $ $D_2: 2x-15=0.$
2.252. An ellipse whose major axes coincide with the coordinate axes passes through the points $M_1(2, \sqrt 3)$ and $M_2(0, 2).$ Write its equation, find the focal radii of point $M_1$ and the distances from this point to the directrices.
Solution.
Since the axes of the ellipse coincide with the coordinate axes, the center of the ellipse coincides with the origin. Therefore, from the fact that the point $(0, 2)$ belongs to the ellipse, we can conclude that $b=2.$
Next, to find $a,$ substitute the found value of $b$ and the coordinates of point $M_1(2, \sqrt 3)$ into the canonical equation of the ellipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1:$
$$\frac{2^2}{a^2}+\frac{(\sqrt 3)^2}{2^2}=1\Rightarrow \frac{4}{a^2}+\frac{3}{4}=1\Rightarrow \frac{4}{a^2}=\frac{1}{4}\Rightarrow a^2=16\Rightarrow a=4.$$
Thus, the equation of the ellipse is $\frac{x^2}{16}+\frac{y^2}{4}=1.$
Next, let's find the coordinates of the foci:
$c=\sqrt{a^2-b^2}=\sqrt{16-4}=2\sqrt 3\Rightarrow F_1(-2\sqrt 3, 0),,,, F_2(2\sqrt 3, 0).$
From here, we find $\overline {F_1M_1}=(2+2\sqrt 3, \sqrt 3),$ $\overline{F_2M_1}=(2-2\sqrt 3, \sqrt 3).$
Consequently, $r_1=|\overline {F_1M_1}|=\sqrt{(2+2\sqrt 3)^2+ (\sqrt 3)^2}=\sqrt{4+8\sqrt 3+12+3}=$ $=\sqrt{16+8\sqrt 3+3}=\sqrt{(4+\sqrt 3)^2}=4+\sqrt 3,$
$r_2=|\overline {F_2M_1}|=\sqrt{(2-2\sqrt 3)^2+ (\sqrt 3)^2}=\sqrt{4-8\sqrt 3+12+3}=$ $=\sqrt{16-8\sqrt 3+3}=\sqrt{(4-\sqrt 3)^2}=4-\sqrt 3.$
To find the distances from point $M_1$ to the directrices, let's find the equations of the directrices using the formulas $D_1: x=-a/e$ and $D_2: x=a/e:$
$e=\frac{c}{a}=\frac{2\sqrt 3}{4}=\frac{\sqrt 3}{2};$
$D_1: x=-\frac{4}{\frac{\sqrt 3}{2}}=-\frac{8}{\sqrt 3}\Rightarrow \sqrt 3 x+8=0;$
$D_2: x=\frac{4}{\frac{\sqrt 3}{2}}=\frac{8}{\sqrt 3}\Rightarrow \sqrt 3 x-8=0.$
The distance from the point $P(x_0, y_0)$ to the line $L: Ax+By+C=0$ is calculated by the formula: $$d=\left|\frac{Ax_0+By_0+C}{\sqrt{A^2+B^2}}\right|.$$
Thus, the distance from the point $M_1(2, \sqrt 3)$ to the line $D_1: \sqrt 3 x+8=0$
$$d_1=\left|\frac{2\sqrt 3+8}{\sqrt{(\sqrt 3)^2}}\right|=\frac{2\sqrt 3+8}{\sqrt 3};$$
The distance from the point $M_1(2, \sqrt{3})$ to the line $D_2: \sqrt{3}x-8=0$
$$d_2=\left|\frac{2\sqrt 3-8}{\sqrt{(\sqrt 3)^2}}\right|=\frac{8-2\sqrt 3}{\sqrt 3}.$$
Answer: $\frac{x^2}{16}+\frac{y^2}{4}=1,$ $r_1=4+\sqrt 3,$ $r_2=4-\sqrt 3,$ $d_1=\frac{8+2\sqrt 3}{\sqrt 3},$ $d_2=\frac{8-2\sqrt 3}{\sqrt 3}.$
Hyperbola.
The hyperbola with the canonical equation $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$, where $a,b>0$, has the form shown in the figure. The parameters $a$ and $b$ are called the semi-axes of the hyperbola. The points $A_1(-a, 0)$, $A_2(a, 0)$ are its vertices. The axes of symmetry $Ox$ and $Oy$ are the real and imaginary axes respectively, and the center of symmetry $O$ is the center of the hyperbola.
The lines $y=\pm\frac{b}{a}x$ are the asymptotes of the hyperbola.
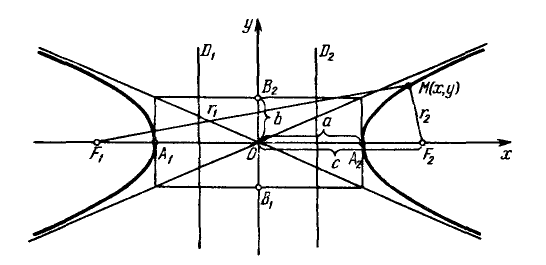
The points $F_1(-c, 0)$ and $F_2(c, 0)$, where $c=\sqrt{a^2+b^2}\geq 0$, are called the foci of the hyperbola. The vectors $\overline{F_1M}$ and $\overline{F_2M}$ are the focal radius vectors, and the numbers $r_1=|\overline{F_1M}|$ and $r_2=|\overline{F_2M}|$ are the focal radii of the point $M$ belonging to the hyperbola.
The number $e=\frac{c}{a}=\sqrt{1+\frac{b^2}{a^2}},, (1
The lines $D_1: x=-a/e$ and $D_2:x=a/e$, perpendicular to the major axis and passing at a distance $a/e$ from the center, are called the directrices of the hyperbola.
Theorem. (The directive property of the hyperbola).
The hyperbola is the locus of points for which the ratio of the distances from the point to the focus and to the corresponding directrix is constant and equal to $e$.
Examples.
2.265. Construct the hyperbola $16x^2-9y^2=144$. Find: a) the semi-axes; b) the coordinates of the foci; c) the eccentricity; d) the equations of the asymptotes; e) the equations of the directrices.
Solution.
Let's rewrite the equation of the hyperbola in canonical form:
$$ 16x^2-9y^2=144 |:144\Rightarrow\frac{16x^2}{144}-\frac{9y^2}{144}=1\Rightarrow$$
$$\Rightarrow\frac{x^2}{9}-\frac{y^2}{16}=1\Rightarrow\frac{x^2}{3^2}+\frac{y^2}{4^2}=1.$$
a) We find the semi-axes: $a=3$, $b=4$.
b) To find the foci, we use the formulas $F_1(-c, 0)$ and $F_2(c, 0)$, where $c=\sqrt{a^2+b^2}$:
$c=\sqrt{3^2+4^2}=\sqrt{25}=5 \Rightarrow F_1(-5, 0), \quad F_2(5, 0)$.
c) The eccentricity is given by $e=\frac{c}{a}=\frac{5}{3}$.
d) The asymptotes of the hyperbola are found using the formulas $y=\pm\frac{b}{a}x$:
$$y=\pm\frac{4}{3}x.$$
d) The equations of the directrices are found using the formulas $D_1: x=-a/e$ and $D_2: x=a/e$:
$D_1: x=-\frac{3}{5/3}=-\frac{9}{5}$ and $D_2: x=\frac{3}{5/3}=\frac{9}{5}$.
Answer: a) $a=3$, $b=4$; b) $F_1(-5, 0)$, $F_2(5, 0)$; c) $e=\frac{5}{3}$; d) $y=\pm\frac{4}{3}x$; d) $D_1: x=-\frac{9}{5}$ and $D_2: x=\frac{9}{5}$.
2.269 (a). Establish that the equation $16x^2-9y^2-64x-54y-161=0$ defines a hyperbola. Find its center $C$, semi-axes, eccentricity, equations of asymptotes, and directrices.
Solution.
Let's bring the given equation to canonical form by completing the squares:
$$16x^2-9y^2-64x-54y-161=(16x^2-64x)-(9y^2+54y)-161=$$
$$16(x^2-4x+4-4)-9(y^2+6y+9-9)-161=16(x-2)^2-64-9(y+3)^2+81-161=$$
$$16(x-2)^2-9(y+3)^2-144=0\Rightarrow16(x-2)^2-9(y+3)^2=144|:144\Rightarrow$$
$$ \frac{(x-2)^2}{9}-\frac{(y+3)^2}{16}=1\Rightarrow\frac{(x-2)^2}{9}-\frac{(y+3)^2}{16}=1.$$
This is the equation of a hyperbola. The center has coordinates $C=(x_0, y_0)=(2,-3)$; the semi-axes are $a=3$ and $b=4$.
$c=\sqrt{a^2+b^2}\Rightarrow c=\sqrt{9+16}=\sqrt {25}=5\Rightarrow e=\frac{c}{a}=\frac{5}{3}$.
The asymptotes of the hyperbola with the center at the origin are found using the formulas $y=\pm\frac{b}{a}x$, and with the center at the point $C=(x_0, y_0)$ - using the formula $y-y_0=\pm\frac{b}{a}(x-x_0)$,
$$y+3=\frac{4}{3}(x-2)\Rightarrow 3y+9=4x-8\Rightarrow 4x-3y-17=0.$$
$$y+3=-\frac{4}{3}(x-2)\Rightarrow 3y+9=-4x+8\Rightarrow 4x+3y+1=0.$$
The equations of the directrices for the ellipse with the center at the origin are found using the formulas $D_1: x=-a/e$ and $D_2: x=a/e$:
$D_1: x=-\frac{3}{5/3}=-\frac{9}{5}$ and $D_2: x=\frac{3}{5/3}=\frac{9}{5}$. Since the center of the given ellipse is shifted, the directrices will have equations $D_1: x=x_0-a/e$ and $D_2: x=x_0+a/e$:
$$D_1: x=2-\frac{9}{5}=\frac{10-9}{5}=\frac{1}{5}\Rightarrow 5x-1=0 $$
$$D_2: x=2+\frac{9}{5}=\frac{10+9}{5}=\frac{19}{5}\Rightarrow 5x-19=0 $$
Answer: $C=(2, -3);$ $a=3,$ $b=4;$ $ e=\frac{5}{3},$ $4x-3y-17=0,$ $4x+3y+1=0,$ $D_1:5x-1=0, $ $D_2: 5x-19=0.$
2.272. Having verified that the point $M(-5, 9/4)$ lies on the hyperbola $\frac{x^2}{16} - \frac{y^2}{9} = 1$, find the focal radii of this point and the distances from this point to the directrices.
Solution.
Let's verify that the given point lies on the hyperbola:
$$\frac{x^2}{16}-\frac{y^2}{9}=1\Rightarrow \frac{(-5)^2}{16}-\frac{(9/4)^2}{9}=\frac{25}{16}-\frac{81}{16\cdot 9}=\frac{25\cdot 9-81}{144}=\frac{144}{144}=1.$$
Therefore, the point $M(-5, 9/4)$ lies on the hyperbola $\frac{x^2}{16} - \frac{y^2}{9} = 1$.
To find the focal radii, we need to determine the foci of the hyperbola:
$c = \sqrt{a^2 + b^2} \Rightarrow c = \sqrt{16 + 9} = \sqrt{25} = 5$. Therefore, the foci have coordinates $F_1(-5, 0), F_2(5, 0)$.
The focal radii of the point can be found using the formulas $r_1 = |\overline{F_1M}|$ and $r_2 = |\overline{F_2M}|$.
$$\overline{F_1M}=(-5-(-5), 9/4)=(0, 9/4)\Rightarrow |\overline{F_1M}=\sqrt{(9/4)^2}|=9/4.$$
$$\overline{F_2M}=(-5-5, 9/4)=(-10, 9/4)\Rightarrow |\overline{F_1M}=\sqrt{10^2+(9/4)^2}|=$$ $$=\sqrt{100+81/16}=\sqrt\frac{1681}{16}=\frac{41}{4}.$$
To find the distances from the point $M$ to the directrices, we will find the equations of the directrices using the formulas $D_1: x = -a/e$ and $D_2: x = a/e$:
$e=\frac{c}{a}=\frac{5}{4};$
$D_1: x=-\frac{4}{5/4}\Rightarrow x=-\frac{16}{5}\Rightarrow 5x+16=0;$
$D_2: x=\frac{4}{5/4}\Rightarrow x=\frac{16}{5}\Rightarrow 5x-16=0;$
The distance from the point $P(x_0, y_0)$ to the line $L: Ax + By + C = 0$ is calculated using the formula$$d=\left|\frac{Ax_0+By_0+C}{\sqrt{A^2+B^2}}\right|.$$
Thus, the distance from the point $M(5, 9/4)$ to the line $D_1: \sqrt 5x + 16 = 0$
$$d_1=\left|\frac{5\cdot 5+16}{\sqrt{5^2}}\right|=\frac{41}{5};$$
The distance from the point $M(5, 9/4)$ to the line $D_2: \sqrt{5}x - 16 = 0$
$$d_2=\left|\frac{5\cdot 5-16}{\sqrt{5^2}}\right|=\frac{9}{5}.$$
Answer: $r_1=9/4,$ $r_2=\frac{41}{4};$ $d_1=\frac{41}{5};$ $d_2=\frac{9}{5}.$
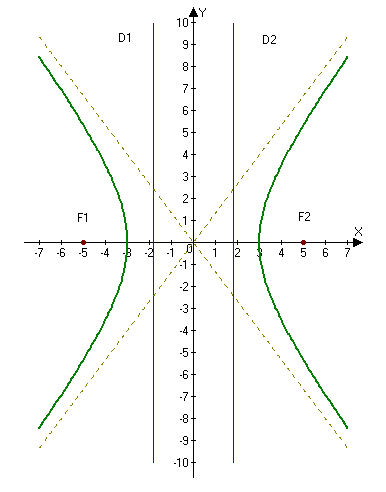
2.273. Find the points on the hyperbola $\frac{x^2}{9} - \frac{y^2}{16} = 1$ that are at a distance of $7$ from the focus $F_1$.
Solution.
From the equation of the hyperbola, we find the semi-axes: $a=3, , b=4.$ Consequently, $c = \sqrt{a^2 + b^2} \Rightarrow c = \sqrt{9 + 16} = \sqrt{25} = 5.$
From here, we find $F_1 = (-5, 0).$
The geometric place of points located at a distance of $7$ from the focus $F_1$ is a circle centered at the point $F_1=(-5, 0)$ with radius $r=7$:
$$(x+5)^2+y^2=7^2.$$
To find the points on the hyperbola $\frac{x^2}{9} - \frac{y^2}{16} = 1$ that are at a distance of $7$ from the focus $F_1$, we solve the system of equations:
$$\left\{\begin{array}{lcl}\frac{x^2}{9}-\frac{y^2}{16}=1\\(x+5)^2+y^2=7^2\end{array}\right.$$
$$\Rightarrow\left\{\begin{array}{lcl}\frac{x^2}{9}-\frac{y^2}{16}=1\\y^2=7^2-(x+5)^2\end{array}\right.\Rightarrow\left\{\begin{array}{lcl}\frac{x^2}{9}-\frac{7^2-(x+5)^2}{16}=1\\y^2=7^2-(x+5)^2\end{array}\right.$$
$$\Rightarrow\left\{\begin{array}{lcl}16x^2-9(49-x^2-10x-25)=144\\y^2=7^2-(x+5)^2\end{array}\right.\Rightarrow$$ $$\Rightarrow\left\{\begin{array}{lcl}16x^2-216+9x^2+90x=144\\y^2=7^2-(x+5)^2\end{array}\right.\Rightarrow$$
$$\Rightarrow\left\{\begin{array}{lcl}25x^2+90x-360=0\\y^2=7^2-(x+5)^2\end{array}\right.\Rightarrow\left\{\begin{array}{lcl}5x^2+18x-72=0\\y^2=7^2-(x+5)^2\end{array}\right.$$
Let's solve the equation $5x^2 + 18x - 72 = 0$:
$D = 18^2 + 4 \cdot 5 \cdot 72 = 324 + 1440 = 1764 = 42^2.$
$x_1 = \frac{-18 + 42}{10} = \frac{24}{10} = 2.4;$ $x_2 = \frac{-18 - 42}{10} = -6.$
Now we find the corresponding $y$ coordinates: $y_1 = \pm \sqrt{24 - 2.4^2 - 10 \cdot 2.4} = \sqrt{-5.76}$ - there are no real roots.
$y_2 = \pm \sqrt{24 - 6^2 + 10 \cdot 6} = \pm 4\sqrt{3}.$
Answer: $(-6, \pm 4\sqrt{3}).$
Parabola.
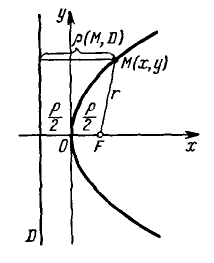
A parabola with the canonical equation $y^2 = 2px, p > 0,$ has the shape shown in the figure.
The number $p$ is called the parameter of the parabola. The point $O$ is its vertex, and the axis $Ox$ is the axis of the parabola.
The point $F\left(\frac{p}{2}, 0\right)$ is called the focus of the parabola, the vector $\overline{FM}$ is the focal radius-vector, and the number $r = |\overline{FM}|$ is the focal radius of the point $M$, belonging to the parabola.
The line $D: x = -\frac{p}{2}$, perpendicular to the axis and passing at a distance $\frac{p}{2}$ from the vertex of the parabola, is called its directrix.
Examples.
2.285 (a). Construct the parabola $y^2 = 6x$ and find its parameters.
Solution.
The parameter $p$ of the parabola can be found from the canonical equation $y^2 = 2px$:
$$y^2=6x\Rightarrow y^2=2\cdot 3x\Rightarrow p=2.$$
Let's make a drawing:
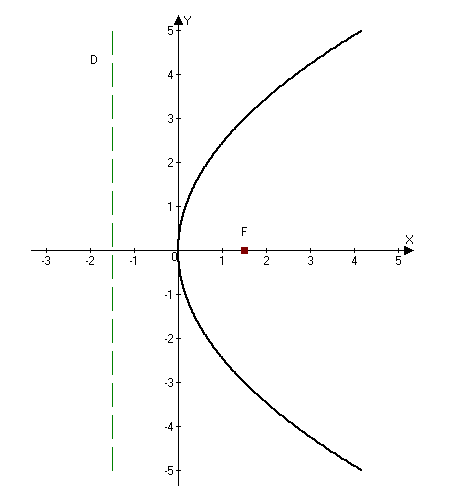
Answer: $p=3.$
2.286 (a). Write the equation of a parabola with its vertex at the origin, knowing that the parabola is located in the left half-plane, symmetrically with respect to the $Ox$ axis, and $p=\frac{1}{2}.$
Solution.
Since the parabola is situated in the left half-plane and is symmetric with respect to the $Ox$ axis, the equation of the parabola will be of the form $y^2 = -2px.$ Substituting the given value of the parameter, we find the equation of the parabola:
$$y^2=-2\cdot\frac{1}{2}x=-x.$$
Answer: $y^2 = -x.$
2.288 (a). Verify that the equation $y^2 = 4x - 8$ defines a parabola, find the coordinates of its vertex $A$, and the value of the parameter $p$.
Solution.
The equation of a parabola, whose center is shifted to the point $(x_0, y_0)$, is of the form $(y - y_0)^2 = 2p(x - x_0)$.
Let's transform the given equation to this form:
$y^2 = 4(x - 2).$
Thus, $y^2 = 4(x^2 - 2)$ represents a parabola with the vertex at the point $(2, 0)$. The parameter $p = 2$.
Answer: $A(2, 0),$ $p=2.$
2.290. Calculate the focal parameter of the point $M$ on the parabola $y^2 = 12x$ if $y(M) = 6.$
Solution.
To find the focal parameter of the point $M$, we need to determine its coordinates. For this, we substitute the $y$ coordinate into the equation of the parabola: $$6^2=12x\Rightarrow 36=12x\Rightarrow x=3.$$
Thus, the point $M$ has coordinates $(3, 6)$.
From the equation of the parabola $y^2 = 12x$, we find the parameter of the parabola: $y^2 = 2 \cdot 6x \Rightarrow p = 6.$ Therefore, the focus of the parabola has coordinates $F(3, 0)$.
Next, we find the focal parameter of the point:
$r = |FM| = \sqrt{(3 - 3)^2 + (6 - 0)^2} = 6.$
Answer: $6.$
2.298. A ray of light is directed from the focus of the parabola $y^2 = 12x$ at an acute angle $\alpha$ to the axis $Ox$, where $tg\alpha = \frac{3}{4}$. Write the equation of the line on which the reflected ray lies.
Solution.
Let's find the focus coordinates. From the canonical equation of the parabola $y^2 = 2px$, we find the parameter: $y^2 = 12x = 2 \cdot 6x \Rightarrow p = 6.$
The focus coordinates are $F(p/2, 0) \Rightarrow F(3,0)$.
Next, we find the equation of the line that passes through the point $(3, 0)$ at an angle $\alpha: tg\alpha = \frac{3}{4}$ to the axis $OX$. We look for the equation in the form $y = kx + b$, where $k = tg\alpha = \frac{3}{4}$.
$y = \frac{3}{4}x + b$
To find $b$, substitute the coordinates of the point $(3, 0)$ into the line equation:
$0=\frac{3}{4}\cdot 3+b\Rightarrow b=-\frac{9}{4}.$ Таким образом, уравнение луча, направленного из фокуса $y=\frac{3}{4}x-\frac{9}{4}.$
Next, let's find the point of intersection of the identified line with the parabola:
$$\left\{\begin{array}{lcl}y=\frac{3}{4}x-\frac{9}{4}\\y^2=12x\end{array}\right.\Rightarrow\left\{\begin{array}{lcl}3x-4y-9=0\\x=\frac{y^2}{12}\end{array}\right.\Rightarrow\left\{\begin{array}{lcl}\frac{3y^2}{12}-4y-9=0\\x=\frac{y^2}{12}\end{array}\right.\Rightarrow$$ $$\left\{\begin{array}{lcl}y^2-16y-36=0\\x=\frac{y^2}{12}\end{array}\right.$$
$$y^2-16y-36=0$$
$$D=256+4\cdot1\cdot36=256+144=400.$$
$$y_1=\frac{16+20}{2}=18\qquad y_2=\frac{16-20}{2}=-2.$$
Since the condition specifies that the ray falls at an acute angle, we only consider the positive coordinate $y = 18$. The corresponding $x$ value is $x = \frac{18^2}{12} = \frac{324}{12} = 27$.
Thus, the ray intersects the parabola at the point $(27, 18)$.
Next, we find the equation of the tangent to the parabola at the found point $(27, 18)$ using the formula $(y - y_0) = y'(x_0)(x - x_0):$
$$y=\sqrt{12x}\Rightarrow y'=\sqrt {12}\frac{1}{2\sqrt x}=\frac{\sqrt 3}{\sqrt{x}}\Rightarrow$$
$$\Rightarrow y'(27)=\frac{\sqrt 3}{\sqrt{ 27}}=\frac{1}{3}.$$
$$y(27)=18.$$
Let's substitute all the found values into the equation of the tangent line:
$y-18=\frac{1}{3}(x-27)\Rightarrow 3y-54=x-27\Rightarrow x-3y+27=0.$
Next, we will find the angle $\beta$ between the ray $y=\frac{3}{4}x-\frac{9}{4}$ and the tangent $x-3y+27=0$. To do this, we will write both equations in the form $y=k_1x+b_1$ and $y=k_2+b_2$. We will calculate the angle using the formula $tg(L_1, L_2)=\frac{k_1-k_2}{1+k_1\cdot k_2}$.
$$L_1: y=\frac{3}{4}x-\frac{9}{4}\Rightarrow k_1=\frac{3}{4};$$
$$L_2: x-3y+27=0\Rightarrow y=\frac{1}{3}x+9\Rightarrow k_2=\frac{1}{3}.$$
$$tg \beta=tg(L_1, L_2)=\frac{\frac{3}{4}-\frac{1}{3}}{1+\frac{3}{4}\frac{1}{3}}=\frac{\frac{5}{12}}{\frac{5}{4}}=\frac{1}{3}.$$
It is easy to see that the angle between the ray $L_1,$ directed from the focus, and its reflection equals $\pi - 2\beta,$ and the angle between the reflected ray and the axis $Ox$ is $\pi - (\pi - 2\beta) - \alpha = 2\beta - \alpha.$
Knowing $tg\beta = \frac{1}{3}$ and $tg\alpha = k_1 = \frac{3}{4}$ and recalling the formulas for the double angle of tangent and the tangent of the difference, we find $tg(2\beta - \alpha):$
$$tg 2\beta=\frac{2tg\beta}{1-tg^2\beta}=\frac{\frac{2}{3}}{1-\frac{1}{9}}=\frac{\frac{2}{3}}{\frac{8}{9}}=\frac{3}{4}.$$
$$tg(2\beta-\alpha)=\frac{tg2\beta-tg\alpha}{1+tg2\beta tg\alpha}=\frac{\frac{3}{4}-\frac{3}{4}}{1+\frac{3}{4}\frac{3}{4}}=0.$$
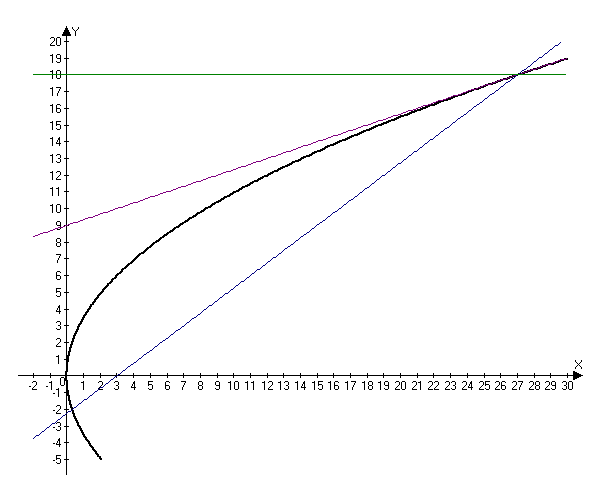
Therefore, the line containing the reflected ray is parallel to the axis $Ox.$ Since it passes through the point $(27, 18),$ we can write its equation as $y=18.$
Answer: $y=18.$


