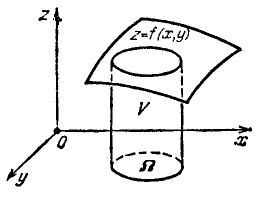
Calculation of areas and volumes using double integrals

The area of the region.

The area of the region $S$, located in the $xy$-plane, is calculated using the formula$$S=\iint\limits_{S}dxdy.$$

Examples.

Find the area bounded by the following curves: $xy=a^2,,, x+y=\frac{5}{2}a,,,,,(a>0).$

Solution.

We find the area of the region using the formula $S=\iint\limits_{S}dxdy.$ To compute the double integral, we first find the points of intersection of the two given curves.

$$\left\{\begin{array}{lcl}xy=a^2\\ x+y=\frac{5}{2}a\end{array}\right. \Rightarrow \left\{\begin{array}{lcl}x=\frac{a^2}{y}\\ \frac{a^2}{y}+y= \frac{5}{2}a\end{array}\right.\Rightarrow \left\{\begin{array}{lcl}x= \frac{a^2}{y}\\ a^2+y^2=\frac{5}{2}ay\end{array}\right.$$

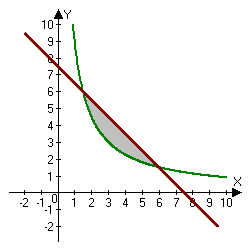
We solve the quadratic equation.

$$y^2-\frac{5}{2}ay+a^2=0$$

$$D=\frac{25}{4}a^2-4a^2=\frac{9}{4}a^2$$

$$y_1=\frac{\frac{5}{2}a+\frac{3}{2}a}{2}=2a,$$

$$y_2=\frac{\frac{5}{2}a-\frac{3}{2}a}{2}=\frac{a}{2}.$$

Accordingly, $$x_1=\frac{a^2}{2a}=\frac{a}{2},$$

$$x_2=\frac{a^2}{\frac{a}{2}}=2a.$$

Now we find the area of the figure:

$$S=\iint\limits_{S}dxdy= \int\limits_{a/2}^{2a}\int\limits_{a^2/x}^{\frac{5}{2}a-x}dxdy= \int\limits_{a/2}^{2a}\left( \frac{5}{2}a-x-\frac{a^2}{x} \right)dx= \left.\left(\frac{5}{2}ax- \frac{x^2}{2}- a^2\ln x\right)\right|_{a/2}^{2a}=$$ $$=\frac{5}{2}2a^2-\frac{4a^2}{2}-a^2\ln (2a)-\frac{5}{2}\frac{a^2}{2}+\frac{a^2}{8}+a^2\ln \frac{a}{2}= 5a^2-2a^2- a^2\ln (2a) -\frac{5a^2}{4}+\frac{a^2}{8}+a^2\ln \frac{a}{2}=$$ $$=\frac{15}{8}a^2-a^2(\ln2+\ln a-\ln a+\ln 2)=\frac{15}{8}a^2-2a^2\ln 2.$$

Answer: $\frac{15}{8}a^2-2a^2\ln 2.$

Example.

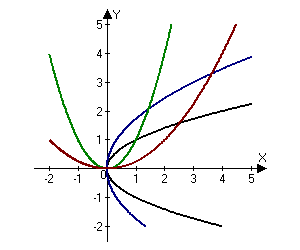
Compute the area of the region bounded by the parabolas:

$$y^2=x,\; y^2=3x,\; x^2=y,\; x^2=4y. $$

Solution.

Let's introduce new coordinates $(u,v):$

$$ y^2=ux,\; x^2=vy,$$

$$ u=\frac{y^2}{x},\; v=\frac{x^2}{y}, $$

So

$$ S=\iint\limits_D\,dxdy = \iint\limits_G \frac{1}{3}\,dudv=\frac{1}{3}\int\limits_1^3du\int\limits_1^4dv=2. $$

Volume of a cylindroid.

The volume of a cylindroid, bounded above by a continuous surface $z=f(x, y)\geq 0$, below by the plane $z=0$, and laterally by the straight cylindrical surface, cutting out from the $xy$-plane a measurable region $\Omega$, is given by$$V=\iint\limits_{\Omega}f(x, y)dxdy.$$